Вывод алгоритма уравнивания параметрическим способом
Необходимо найти такой вектор х , чтобы он был несмещ-ой, дост-ой и эффект-ой оценкой. Поскольку вектор х есть вектор поправок в приближенные значения координат, то и корд-ты будут несмещ-мии эффек-ми, т.е. наиболее точными. Вывод алгоритма уравнивания будем вести на основе оценки функции уравненных значений параметров х и измерен.Для вывода алгоритма уравнивания представим в начале уравнение поправок в матричном виде:
V 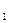 =a
=a 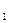 δx
δx 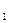 +b
+b 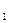 δx
δx 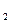 +…+w
+…+w 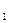 δx
δx 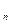 +l
+l 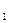 , P
, P 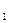
V 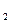 =a
=a 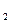 δx
δx 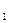 +b
+b 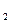 δx
δx 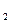 +…+w
+…+w 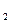 δx
δx 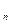 +l
+l 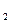 , P
, P 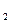
V 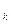 =a
=a 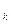 δx
δx 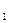 +b
+b 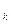 δx
δx 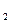 +…+w
+…+w 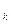 δx
δx 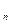 +l
+l 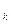 , P
, P 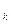
Каждому измерению должен соответствов. определенный вес.
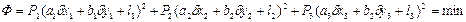
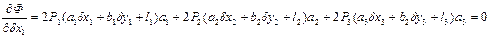
если 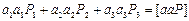 то
то 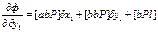 Получают систему уравнений
Получают систему уравнений 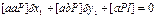 ;
; 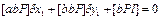 Из этих уравнений находят поправки
Из этих уравнений находят поправки 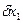 и
и 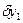
Матричный способ: алгоритм уравнивания параметрическим способом заключается в следующем: а) составляется система уравнений поправок V=A*X+L, V= 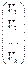 X=
X= 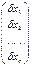 L=
L= 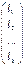 A=
A= 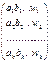 Р=
Р= 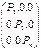 б) вычисляется матрица нормальных уравнений N = АT РА;в) находится вектор параметров X=-N-1AT РLНастоящий алгоритм можно вывести и на основе метода наименьших квадратов. Согласно этому методу должно выполняться условие: VTPV=min, V=AX+L. Неиз-н вектор Х? Ф= VTPV, ∂Ф/∂х=2VTP
б) вычисляется матрица нормальных уравнений N = АT РА;в) находится вектор параметров X=-N-1AT РLНастоящий алгоритм можно вывести и на основе метода наименьших квадратов. Согласно этому методу должно выполняться условие: VTPV=min, V=AX+L. Неиз-н вектор Х? Ф= VTPV, ∂Ф/∂х=2VTP 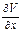 =0, ∂Ф/∂х=2VTPA=0, VTPA=0, (VTPA)T=0, ATPV=0, ATP(AX+L)=0, ATPAХ+ ATPL=0, ATPA=N, NХ+ATPL=0, NХ=-ATPL. Для вычисления умножим эту матрицу на N-1слева. N-1 Nx=- N-1 ATPL, Х=- N-1 ATPL
=0, ∂Ф/∂х=2VTPA=0, VTPA=0, (VTPA)T=0, ATPV=0, ATP(AX+L)=0, ATPAХ+ ATPL=0, ATPA=N, NХ+ATPL=0, NХ=-ATPL. Для вычисления умножим эту матрицу на N-1слева. N-1 Nx=- N-1 ATPL, Х=- N-1 ATPL
Таким образом, алгоритм уравнивания параметрическим способом заключается в следующем:
а) составляется система уравнений поправок V=A*X+L
б) вычисляется матрица нормальных уравнений N = АT РА;
в) находится вектор параметров X=-N-1AT РLи оценивается его точность DX= σ2 N-1
Дата добавления: 2021-12-14; просмотров: 660;











