Общие сведения о синтезе системы электропривода

При проектировании СЭП решаются два типа задач: задачи синтеза и задачи анализа. Как правило, при анализе системы осуществляется ее моделирование. Структурная схема (СС) системы электропривода, являющаяся одной из форм представления математической модели системы автоматического управления (САУ), служит основой для моделирования. Другая форма представления математической модели (ММ) системы – это уравнения состояния, которые связаны со структурной схемой.

Структурная схема изображается так, чтобы управляющее воздействие находилось в левой части чертежа. Тогда условно можно считать, что при моделировании процесс реализуется сначала для звена СС, изображенного в левой части, а далее для других звеньев, находящихся правее, т.е. решение задачи осуществляется «слева – направо». Процесс составления инверсных уравнений при функциональном синтезе начинается с крайнего правого звена структурной схемы системы (ССС) и продолжается для других звеньев, расположенных на изображении СС левее, т.е. задача решается в направлении «справа – налево».

При составлении инверсных уравнений исходным материалом служит ССС, которая модифицируется в детализированную структурную схему системы (ДССС), состоящую только из типовых динамических звеньев (пропорционального, дифференцирующего и интегрирующего), узлов сравнения (сумматоров) и нелинейных звеньев. Для этого все «сложные» динамические звенья ССС, такие как апериодическое, колебательное и др. заменяются эквивалентными структурами, состоящими только из пропорциональных, дифференцирующих и интегрирующих звеньев. Таким образом, представляя систему электропривода в виде пропорциональных, дифференцирующих и интегрирующих звеньев, можно использовать для решения задач математические операции умножения (деления), дифференцирования и интегрирования.

С практической точки зрения решение задачи синтеза сложнее по сравнению с задачами анализа. При анализе СЭП в процессе цифрового моделирования, независимо от того, в какой форме представлена ММ САУ, решается система дифференциальных уравнений состояния. Известно, что общим методом решения дифференциальных уравнений является их интегрирование. В математических программных пакетах (например, Matlab) этот процесс реализуется на основе численных методов интегрирования дифференциальных уравнений. В процессе интегрирования все возникающие «сигналы – помехи» сглаживаются и их влияние на результаты моделирования незначительно. При использовании численных методов синтеза приходится в отличие от задач анализа применять другую математическую операцию – дифференцирование. В этом случае влияние «сигналов – помех» усиливается во много раз.

В данной работе делается попытка использования пакета Simulink (для решений задач функционального синтеза СЭП и исследования инверсных структур и анализа полученных результатов. Первым звеном ССС, которое подвергается синтезу, является звено, которое характеризует процесс в механической части СЭП (рис. 1).

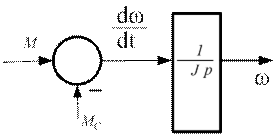
Рис. 1. Структурная схема механической части СЭП

Уравнение, соответствующее этой структуре, является наиболее часто используемым при описании большинства электроприводов.

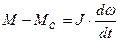. (1)

Для определения угловой скорости вращения 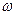используется операция интегрирования .

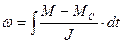Инверсное уравнение для вычисления момента двигателя по заданной временной зависимости угловой скорости можно получить из (1).

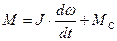. (2)

Отсюда следует инверсное уравнение в операторной форме.

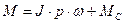. (3)

Уравнению (3) соответствует следующая инверсная структура (рис. 2).

По инверсной структуре составлена программа расчета в программном пакете Simulink (Matlab) (рис. 3). На первом этапе при исследовании метода синтеза механической части СЭП в пакете Simulink принят вариант заданной зависимости скорости от времени , состоящий из двух линейных участков (рис. 4).

Для моделирования заданной зависимости скорости от времени использованы блок «Ramp» (линейное нарастание) и блок «Насыщение» из библиотек Simulink.

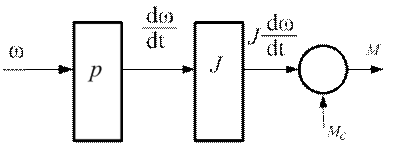
Рис. 2. Инверсная структурная схема механической части СЭП

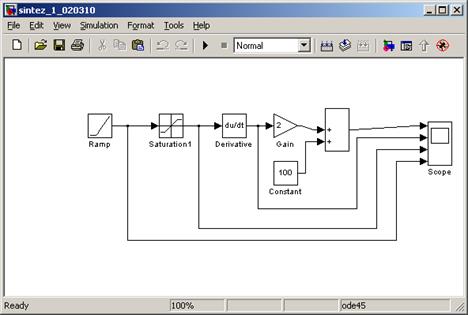
Рис. 3. Программа исследования инверсной структурной схемы механической части СЭП (J=2; M_C=100 Нм)

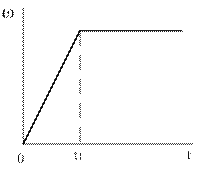
Рис. 4. Заданная зависимость скорости от времени

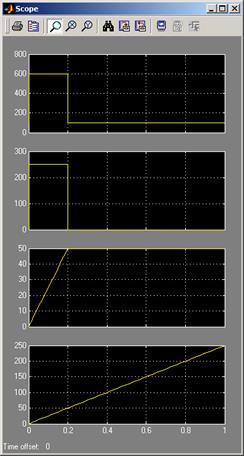
Рис. 5. Результаты синтеза механической части СЭП

На рис.5 представлены четыре графика. На первом (верхнем) графике приведена зависимость момента двигателя 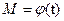. На втором графике показана зависимость сигнала на выходе дифференцирующего звена. Заданная зависимость скорости от времени представлена на третьем графике.

На рис.6 приведена инверсная структурная схема СЭП с двигателем постоянного тока независимого возбуждением.

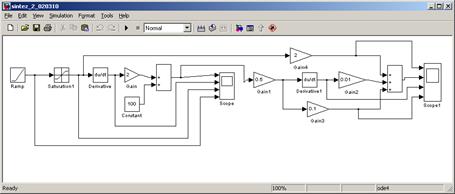
Рис. 6. Программа исследования инверсной структурной схемы СЭП с двигателем постоянного тока независимого возбуждением

На рис.7 представлены результаты синтеза СЭП с двигателем постоянного тока независимого возбуждением

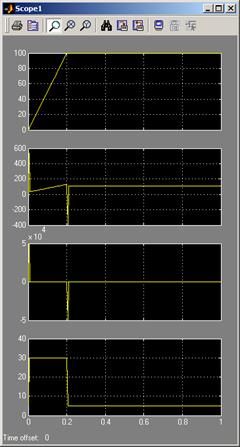
Рис. 7. Результаты синтеза СЭП с двигателем постоянного тока независимого возбуждением

Обобщенный алгоритм синтеза нелинейных АСУ ЭП на ЭВМ включает в себя три основные задачи: а) функциональный синтез, в ходе которого при заданной структуре и параметрах звена или системы в целом определению подлежит функция управления на входе звена или системы; б) параметрический синтез, в ходе которого при заданных структуре и входном воздействии на звено определению подлежат искомые параметры звена (или группы звеньев); в) структурно-параметрический синтез, в ходе которого при заданных законах измерения координат на входе и выходе элементарного звена определению подлежат структура, характеристики и параметры звена, а при заданной основной структуре звена - число, вид и место включения дополнительных связей, реализующих заданную передаточную функцию звена.

В ходе синтеза того или иного звена, и особенно всей систему целом, указанные выше основные задачи приходится, как правило решать взаимосвязано, т. е. варьировать возможные решения, добиваясь оптимального, наиболее простого и физически реализуемого. Синтез ведется позвенно, от выхода к входу системы на базе инверсии алгоритма последовательного типа, используемого при решении уравнений состояния (численном интегрировании уравнений состояния по методу А. В. Башарина).