Численное интегрирование дифференциальных уравнений математической модели системы электропривода методом Эйлера

Численное интегрирование уравнений состояния по методу Эйлера рассмотрим на примере уравнения состояния для механической части СЭП.

Из курса высшей математики известно, что

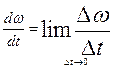. (9)

С учетом выражения (9) запишем уравнение (7) в дискретной форме и используем понятия, связанные с конечными разностями.

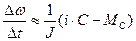. (10)

Первая прямая разность угловой скорости равна 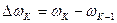. (11)

Из уравнения (11) следует, что решение дифференциального уравнения (6) будет равно 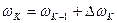. (12)

Угловую скорость с учетом уравнений (10) и (11) вычисляют по следующей формуле.

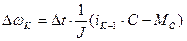. (13)

Уравнения (10) - (13) определяют суть метода Эйлера при численном интегрировании дифференциального уравнения математической модели системы электропривода.

Аналогично выполняется численное интегрирование дифференциального уравнения при вычислении тока при использовании выражения (6).

Шаг интегрирования 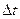устанавливается равным в соответствии с теоремой Котельникова-Шеннона.

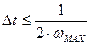, (14)

где – максимальная частота спектра сигнала в системе электропривода.

На этапе проектирования СЭП величину определить достаточно сложно. Поэтому, предлагается методика расчета шага интегрирования 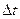по эмпирической формуле.

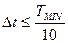, (15)

где 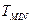- минимальная постоянная времени СЭП.

Уменьшая величину шага интегрирования 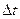, можно снизить погрешность интегрирования, но при этом увеличивается время численного интегрирования дифференциальных уравнений, что в настоящее время не является критичным, т.к. при высоком быстродействии современных вычислительных машин легко преодолевается этот недостаток.

В стандартных программных пакетах, как правило, используется метод Рунге-Кутта, являющийся методом 4-го порядка точности.