Функциональный синтез разомкнутой системы электропривода при управлении пуском
 |
При формировании переходных процессов в электроприводах (ЭП) возникает необходимость решения задачи определения управляющего воздействия системы управления ЭП. В практике управления пуском электропривода широко применяется линейный закон изменения скорости двигателя или рабочего органа, представленный на рис. 8. Ориентировочно при анализе такого варианта формирования переходного процесса без учета «электромагнитной инерции» предполагается, что закон изменения управляющего воздействия также будет линейным. Очевидно, что фактически он будет отличаться от линейного, если учитывать переходные процессы в цепях якоря двигателя постоянного тока или статора и ротора асинхронного двигателя.
Рис. 8. Линейный закон изменения скорости двигателя
Рассмотрим методику определения управляющего сигнала при линейном пуске для разомкнутой системы электропривода (СЭП) по схеме "силовой преобразователь – двигатель постоянного тока" (СП-ДПТ), приведенной на рис. 9. По классификации, предложенной А. В. Башариным, подобные задачи относятся к группе функционального синтеза. Для реализации функционального синтеза СЭП используем численный метод А. В. Башарина, основанный на применении инверсных уравнений.
 |
Рис. 9. Блок-схема СЭП
Силовой преобразователь (СП) обладает нелинейной характеристикой, которая может быть аппроксимирована двумя отрезками прямых.
Уравнения состояния СЭП для первого линейного участка характеристики силового преобразователя составлены с учетом инерционности СП.
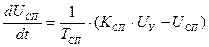 ; (1)
; (1)
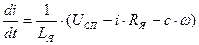 ; (2)
; (2)
 , (3)
, (3)
где 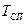 -постоянная времени силового преобразователя;
-постоянная времени силового преобразователя;
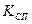 -коэффициент передачи силового преобразователя на первом линейном участке его характеристики;
-коэффициент передачи силового преобразователя на первом линейном участке его характеристики;
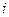 -ток якоря ДПТ с независимым возбуждением;
-ток якоря ДПТ с независимым возбуждением;
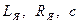 -индуктивность, сопротивление якоря и постоянная ДПТ;
-индуктивность, сопротивление якоря и постоянная ДПТ;
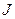 -момент инерции механической части СЭП;
-момент инерции механической части СЭП;
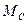 -момент нагрузки ДПТ. В работе принято, что
-момент нагрузки ДПТ. В работе принято, что 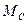 =const.
=const.
По уравнениям состояния построена детализированная структурная схема СЭП, представленная на рис. 10.
 |
Рис. 10. Детализированная структурная схема СЭП
Алгоритм метода функционального синтеза основан на последовательном поэлементном определении входных воздействий звеньев системы от выхода к ее входу. Для синтеза используется математический аппарат инверсных уравнений, которые получают, используя решения уравнений состояния системы численным методом. При этом принимается, что выходной сигнал предыдущего (т.е. j-1) звена является управляющим воздействием на следующее j звено. Входное воздействие на следующее j звено (ΣX(j)ВХ) складывается из управляющего воздействия XJ-1, возмущающего воздействия FВОЗМ и суммарного воздействия обратных связей на j звено (-ΣX(j), m, i). Методика составления инверсных уравнений применительно к алгоритму функционального синтеза подробно изложена в литературе.
Сигнал на входе 5 звена  равен
равен 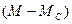 .
.
Тогда 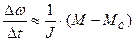 ; (4)
; (4)
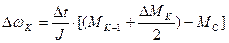 ; (5)
; (5)
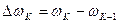 ,
,
где 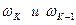 - значения скорости ЭП на «К» и «К-1» шаге интегрирования;
- значения скорости ЭП на «К» и «К-1» шаге интегрирования;
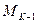 - значение момента электрического двигателя (ЭД) на «К-1» шаге интегрирования;
- значение момента электрического двигателя (ЭД) на «К-1» шаге интегрирования;
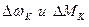 - приращения скорости и момента ЭД на «К» шаге интегрирования.
- приращения скорости и момента ЭД на «К» шаге интегрирования.
Приращение скорости рассчитано с использованием последовательного численного метода интегрирования, предложенного А. В. Башариным. 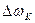 определяется по графику на рис. 1 по формуле
определяется по графику на рис. 1 по формуле 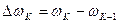 . Так как этот график записывается в память ЭВМ в виде двух массивов узловых точек, то для расчета промежуточных значений применяется простой метод линейной интерполяции. Из выражения (4) можно найти
. Так как этот график записывается в память ЭВМ в виде двух массивов узловых точек, то для расчета промежуточных значений применяется простой метод линейной интерполяции. Из выражения (4) можно найти 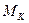 . С этой целью модифицируется формула (4).
. С этой целью модифицируется формула (4). 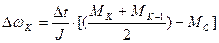 .
.
 . (6)
. (6)
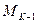 на начальном шаге синтеза принимается равным нулю. Теперь можно найти приращение момента ЭД.
на начальном шаге синтеза принимается равным нулю. Теперь можно найти приращение момента ЭД. 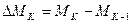
После определения 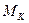 и
и 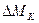 следует переходить к расчету входного воздействия на 4 звено. Поскольку звено 4 является пропорциональным, эта операция не представляется трудной.
следует переходить к расчету входного воздействия на 4 звено. Поскольку звено 4 является пропорциональным, эта операция не представляется трудной.
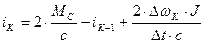 . (7)
. (7)
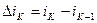 . (8)
. (8)
Уравнение для 3 звена позволяет определить входное воздействие на это звено.
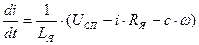 . (9)
. (9)
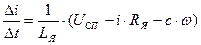 . (10)
. (10)
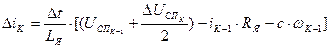 . (11)
. (11)
Далее определяется 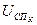 .
.
С этой целью модифицируется формула (11).
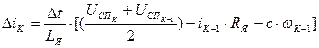 (12)
(12)
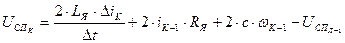 (13)
(13)
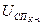 на начальном шаге синтеза принимается равным нулю.
на начальном шаге синтеза принимается равным нулю.
После этой операции можно найти приращение 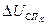 .
.
 (14)
(14)
Так как звено 2 является безинерционным, то значение 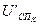 определяется по заданной нелинейной характеристике с применением линейной интерполяции, задаваясь расчетным значением
определяется по заданной нелинейной характеристике с применением линейной интерполяции, задаваясь расчетным значением 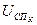 по формуле (13). Нелинейная характеристика может быть представлена в аналитической форме и тогда расчет
по формуле (13). Нелинейная характеристика может быть представлена в аналитической форме и тогда расчет 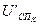 производится без использования интерполяции.
производится без использования интерполяции.
Уравнение для 1 звена (формула (1) 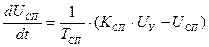 позволяет вычислить напряжение управления
позволяет вычислить напряжение управления 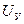 . Для этого представим уравнение (1) в разностной форме по методу Башарина.
. Для этого представим уравнение (1) в разностной форме по методу Башарина.
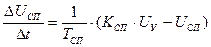 . (15)
. (15)
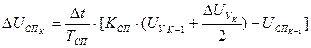 . (16)
. (16)
Инверсное уравнение получим из (16) после его модификации.
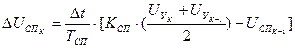 . (17)
. (17)
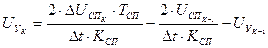 . (18)
. (18)
Уравнение (18) позволяет определить закон изменения управляющего воздействия по заданному графику скорости ЭД.
Расчет задающего воздействия следует выполнить на определенном интервале времени. Выбор шага интегрирования производится в соответствии с рекомендациями.
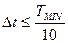 ,
,
где 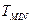 – минимальная постоянная времени звеньев системы управления.
– минимальная постоянная времени звеньев системы управления.
Алгоритм расчета основан на математической модели синтеза системы управления. Блок – схема алгоритма (рис. 11) включает блоки, выполняющие интерполяцию, и блоки, осуществляющие вычисления по формулам (6), (7), (8), (13), (14) и (18). Все вычисления производятся в цикле. Расчет завершается при достижении заданного интервала времени.
 |
Рис. 11. Блок – схема алгоритма синтеза СЭП
Дата добавления: 2020-10-25; просмотров: 695;











