Функциональный синтез системы электропривода с отрицательной обратной связью

В параграфе 19.3 была рассмотрена задача функционального синтеза при пуске электропривода без обратных связей (ОС) по заданному закону. При наличии отрицательной обратной связи, например по скорости, закон изменения задающего напряжения 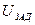будет отличаться от закона изменения скорости двигателя. Для сравнения результатов для этого случая с вариантом системы электропривода (СЭП) без ОС была разработана методика определения управляющего сигнала при линейном пуске для замкнутой системы электропривода (СЭП) по схеме "силовой преобразователь – двигатель постоянного тока с отрицательной обратной связью по скорости" (СП-ДПТ с ООСС), приведенной на рис. 12. Регулятор скорости на этом рисунке представлен узлом сравнения (УС) и вычислителем регулятора скорости (ВРС). Для функционального синтеза СЭП используется численный метод А. В. Башарина.

Силовой преобразователь (СП) обладает нелинейной статической характеристикой управления, которая может быть представлена четырьмя участками (рис. 13).

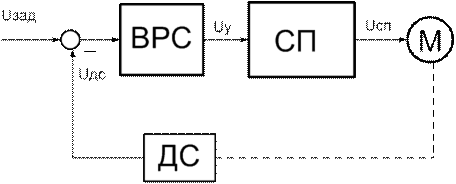
Рис. 12. Блок-схема СЭП с ООСС

Уравнение для первого и второго участков характеристики СП соответствует напряжению управления в интервалах от 0 до 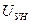(первый участок) и от 0 до – 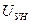(второй участок).

,

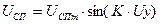где 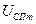-максимальное выходное напряжение СП; 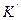- фазовый коэффициент СП. , .

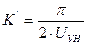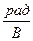Уравнение для третьего участка характеристики СП составляется для напряжения управления больше чем . .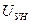

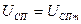Уравнение для четвертого участка характеристики СП отличается от уравнения для третьего участка только знаком и составляется для напряжения управления меньше чем - . .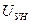

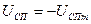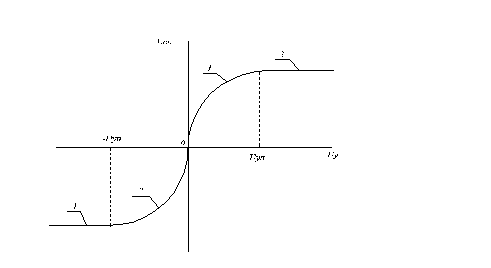
Рис. 13. Характеристика управления реверсивного СП

Инерционность СП учитывается включением в детализированную структурную схему математической модели СЭП (рис. 14) апериодического звена с единичным коэффициентом передачи и передаточной функцией 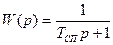. Регулятор скорости принят пропорционально – интегральным. Датчик скорости в модели также представлен апериодическим звеном.

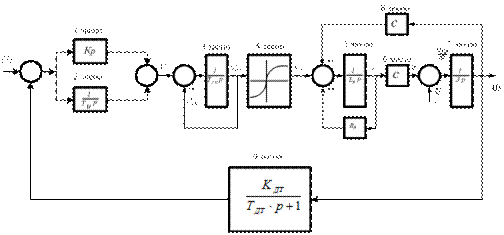
Рис. 14. Структурная схема математической модели СЭП с ООСС

Уравнения для переменных СЭП составлены с учетом возможности получения инверсных формул.

Алгоритм метода функционального синтеза основан на последовательном поэлементном определении входных воздействий звеньев системы от выхода к ее входу.

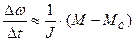; (19)

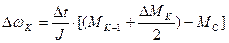; (20)

,

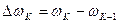где 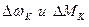- приращения скорости и момента ЭД на « » шаге интегрирования.

Приращение скорости 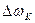определяется по графику на рис. 1 по формуле 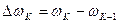. Из выражения (20) можно найти значение . .

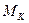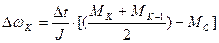. (21)

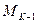на начальном шаге синтеза принимается равным нулю. Теперь можно найти приращение момента ЭД.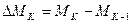

Затем определяется 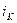(значение тока двигателя на « » шаге интегрирования и приращение тока на этом же интервале – сигнал на входе 6 звена).

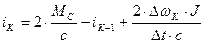. (22)

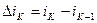. (23)

Уравнение для 5 звена позволяет определить входное воздействие на это звено.

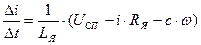. (24)

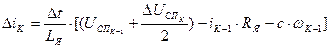. (25)

Далее определяется .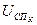

С этой целью модифицируется формула (25).

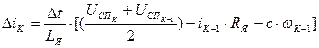(26)

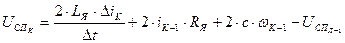(27)

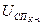на начальном шаге синтеза принимается равным нулю.

После этой операции можно найти приращение .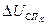

Так как звено 4 является безинерционным, то значение 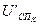определяется по нелинейной характеристике, задаваясь расчетным значением 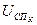по формуле (27).

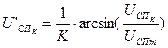(28)

Уравнение для 3 звена позволяет вычислить напряжение управления 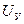. Для этого представим это уравнение в разностной форме по методу Башарина.

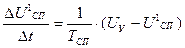. (29)

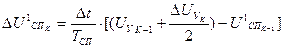. (30)

Инверсное уравнение для 3 звена получим из (30) после его модификации.

. (31)

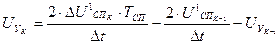. (32)

Входные сигналы для 1 ( 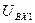) и 2 ( 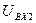)звеньев равны, а выходные отличаются. Поэтому задачу нахождения входного сигнала для этих звеньев можно решить методом последовательных приближений.

Метод вычисления 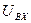базируется на решении системы линейных алгебраических уравнений, составленных на основе разностных уравнений для 1 и 2 звеньев. Результаты решения позволяют точно рассчитать входное воздействие на звенья ПИ-регулятора и выходные сигналы его пропорциональной и интегральной частей.

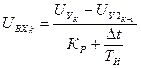. (33)

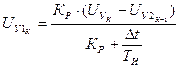. (34)

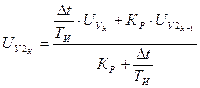. (35)

Задающее воздействие на « » шаге интегрирования зависит от и . .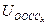

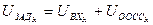Сигнал отрицательной обратной связи по скорости 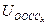находится по решению дифференциального уравнения для датчика скорости (6).

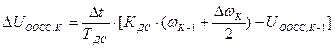. (36)

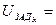
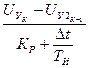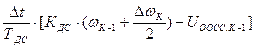+ . (37)

Уравнение (37) является математической записью алгоритма управления пуском ЭД по линейному закону изменения скорости в замкнутой системе электропривода по схеме СП-ДПТ с ООСС.

Расчет задающего воздействия следует выполнить на определенном интервале времени. Выбор шага интегрирования производится в соответствии с рекомендациями.

,

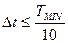где 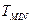– минимальная постоянная времени звеньев системы управления.

Алгоритм расчета основан на математической модели синтеза системы управления. Блок – схема алгоритма включает блоки, выполняющие интерполяцию, и блоки, осуществляющие вычисления по формулам (3-4), (9-10) и (14-18). Все вычисления производятся в цикле. Расчет завершается при достижении заданного интервала времени. Программа может быть составлена на любом языке высокого уровня.