Функциональный синтез системы электропривода с подчиненным

Регулированием

В параграфе 19.4 была рассмотрена задача функционального синтеза системы электропривода (СЭП) с отрицательной обратной связью по скорости (ООСС). Задача решалась для системы, в которой реализован только один регулятор (по скорости). В системах подчиненного регулирования число обратных связей увеличивается. На рис. 15 представлена функциональная схема подчиненной СЭП с двумя регуляторами (по току и по скорости).

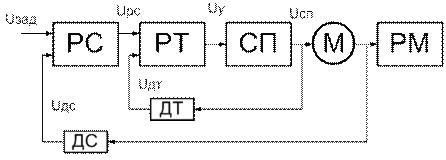
Рис. 15. Функциональная схема подчиненной СЭП с двумя регуляторами (по току и по скорости)

Рассмотрим процесс реализации функционального синтеза для подчиненной СЭП с регуляторами тока и скорости и с двигателем постоянного тока независимого возбуждения (ДПТ с НВ). Силовой преобразователь (СП) обладает нелинейной статической характеристикой управления, которая может быть представлена четырьмя участками. Регуляторы тока и скорости на структурной схеме модели (рис. 16) представлены узлами сравнения УСТ, УСС и вычислителями регуляторов ВРТ, ВРС. Структура регуляторов предполагает реализацию ПИ – законов регулирования.

Для функционального синтеза СЭП используется численный метод А. В. Башарина. Для получения инверсных уравнений сначала составляются уравнения состояния для координат СЭП. С этой целью структурная схема модели подчиненной СЭП выполняется на основе простых динамических звеньев.

Подготовка инверсных уравнений выполняется в следующем порядке. Для каждого звена системы определяется входное воздействие. Расчет начинается для выходного звена и продолжается в направлении от выхода к входу СЭП. В данном случае сначала находится входное воздействие для девятого звена. С этой целью задается в качестве исходной временная зависимость изменения скорости двигателя 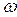. Дифференциальное уравнение для рассматриваемого звена преобразуется в уравнение в конечных разностях.

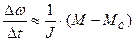. (38)

Затем определяется уравнение для расчета 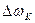в произвольный интервал времени « » по методу Эйлера (2). На его основе находится выражение для приращения скорости по методу А. В. Башарина (3).

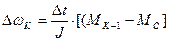. (39)

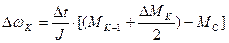; (40)

,

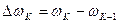где 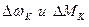- приращения скорости и момента ЭД на « » шаге интегрирования.

Если момент нагрузки 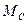изменяется во времени, то это также должно быть учтено при расчете 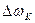(41).

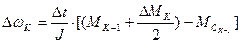. (41)

При функциональном синтезе приращение скорости 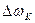фактически определяется по формуле 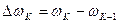с использованием графика 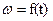. Так как график зависимости 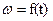в программе синтеза задается в виде двух массивов (массив « 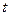» и массив « 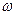»), то для расчета 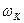и 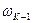используется любой из методов интерполяции (например, линейной интерполяции). Временная ось разбивается на равные отрезки 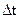, называемые шагами интегрирования. Шаги 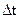нумеруются, начиная с единицы. Тогда произвольное время 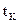можно найти, как 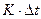. Чем меньше 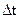, тем точнее выполняется функциональный синтез.

Уравнение (3) можно модифицировать по правилам, изложенным в литературе.

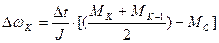. (42)

Из выражения (42) можно найти значение момента двигателя на « » шаге интегрирования .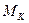

Затем можно найти приращение момента ЭД.

.

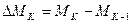Так как момент ДПТ с НВ прямо пропорционален току двигателя ( 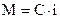), то поэтому легко определяется 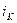(значение тока двигателя на « » шаге интегрирования, т.е. сигнал на входе 8 звена) и приращение тока на этом же интервале .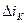

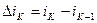. (43)

Далее в конечных разностях составляется уравнение для 7 звена, что позволяет определить входное воздействие на это звено.

Затем определяется уравнение для расчета 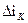в произвольный интервал времени « » по методу Эйлера. На его основе находится выражение для приращения тока по методу А. В. Башарина.

Выражение для 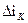модифицируется и после преобразований находится напряжение силового преобразователя .

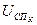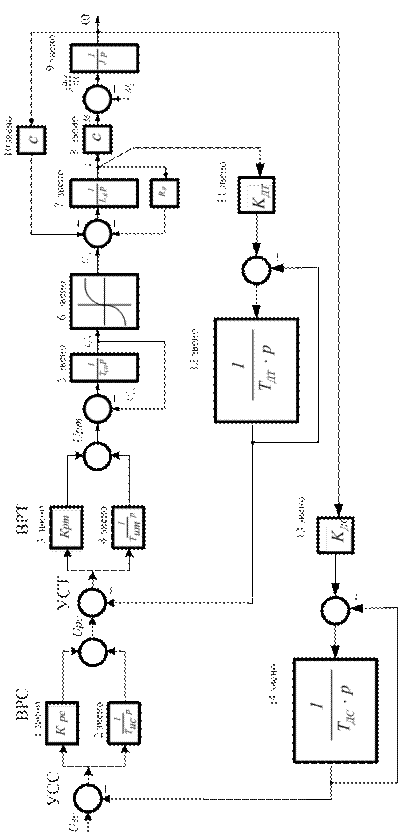
Рис. 16. Структурная схема математической модели СЭП с регуляторами тока и скорости

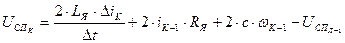. (44)

Далее можно найти приращение напряжения силового преобразователя .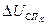

Так как шестое звено является безинерционным, то входной сигнал 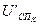для этого звена определяется по нелинейной характеристике, если задаться расчетным значением выходного сигнала 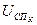по формуле (44).

Уравнение для пятого звена позволяет вычислить выходное напряжение регулятора тока 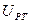. С этой целью сначала решение прямого уравнения для пятого звена представляется в разностной форме по методу Башарина и после его преобразования находится инверсное уравнение .

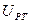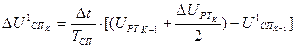. (45)

Инверсное уравнение для 5 звена получим из (8) после его модификации.

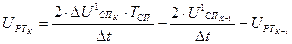. (46)

Входные сигналы для 3 ( 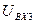) и 4 ( 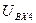) звеньев регулятора тока равны, т.к. соответствуют одному и тому же источнику сигнала 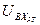, а выходные отличаются.

Метод вычисления 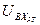базируется на решении системы трех линейных алгебраических уравнений с тремя неизвестными 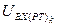, , 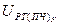, 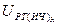составленных на основе разностных уравнений для 3 и 4 звеньев.

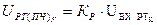; (47)

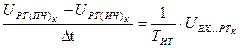; (48)

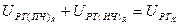. (49)

Результаты решения этих уравнений позволяют точно рассчитать входное воздействие 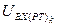на звенья ПИ-регулятора тока и выходные сигналы его пропорциональной 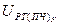и интегральной 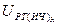частей.

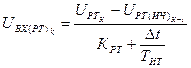. (50)

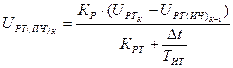. (51)

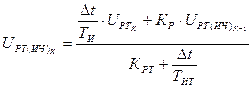. (52)

Сигнал отрицательной обратной связи по току 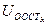находится по решению дифференциального уравнения для датчика тока.

.

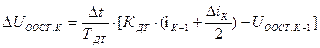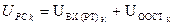
По аналогичной методике находятся входное воздействие 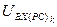на звенья ПИ-регулятора скорости и выходные сигналы его пропорциональной 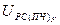и интегральной 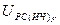частей.

Задающее воздействие зависит от 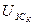и . .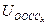

.

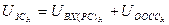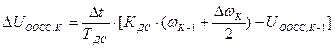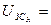
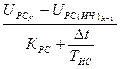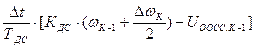+ . (53)

Выражение (53) позволяет обеспечить заданный закон изменения скорости при пуске двигателя в СЭП по схеме «СП-ДПТ с ООСТ и ООСС».

Шаг интегрирования выбирается по условию .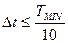

Использование методик функционального синтеза дает возможность применять стандартные приемы формирования оптимальных переходных процессов для различных координат СЭП. Для электропривода по схеме подчиненной СЭП с тремя регуляторами (по току, по скорости и по положению) структурно-параметрический синтез позволит обеспечить требуемый апериодический переходный процесс по положению.