Уравнения статора и ротора АД в векторной форме

Уравнение для цепи статора с применением обобщенных векторов тока, напряжения и потокосцепления в неподвижной системе координат « 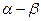» имеет следующий вид.

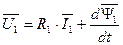. (91)

На основании выражения (55) представим обобщенные вектора тока, напряжения и потокосцепления в уравнении (91) комплексными векторами, записанными в алгебраической форме.

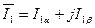. (92)

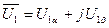. (93)

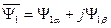. (94)

Подставим выражения (92), (93) и (94) в уравнение (91).

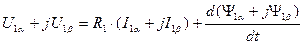. (95)

Раскрывая скобки, преобразуя алгебраическое выражение и приравнивая действительные и мнимые части в правой и левой частях выражения (95) получим два уравнения для цепи статора:

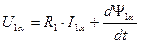. (96)

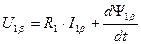. (97)

Уравнение ротора в векторной форме в неподвижной системе координат статора « 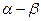» выглядит так.

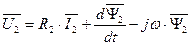. (98)

На основании выражения (55) представим обобщенные вектора тока, напряжения и потокосцепления в уравнении (98) комплексными векторами, записанными в алгебраической форме.

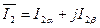. (99)

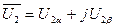. (100)

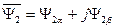. (101)

Подставим выражения (99), (100) и (101) в уравнение (98).

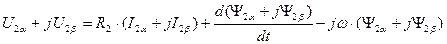. (102)

Раскрывая скобки, преобразуя алгебраическое выражение и приравнивая действительные и мнимые части в правой и левой частях выражения (102) получим два уравнения для цепи ротора:

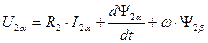. (103)

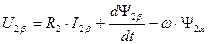. (104)