Подготовка уравнений модели короткозамкнутого АД при частотном управлении

Асинхронный привод с частотным управлением является в настоящее время наиболее распространенным. Однако его динамика чаще всего исследуется с помощью упрощенных моделей с отклонениями в малом. Векторная модель АД позволяет получить точную структурную схему, которую затем можно исследовать современными средствами компьютерного моделирования. Рассмотрим на этом примере методику получения передаточных функций сложных объектов с помощью векторных уравнений ОЭМ. Пусть система координат модели АД ориентирована по вектору напряжения статора с частотой питания 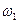, т.е. вращается с угловой скоростью, равной 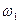. Тогда угловая частота вращения системы координат модели АД в уравнениях (118) и (119) будет определяться частотой сети 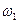, т.е. .

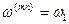Система координат « 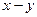», вращающаяся синхронно с потокосцеплением ротора ( 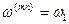при одной паре полюсов) и ориентированная по его направлению, наиболее пригодна для описания процессов в АД.

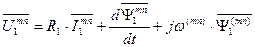. (118)

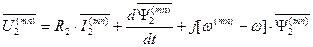. (119)

Из выражений с учетом того, что 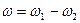, а следовательно 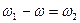получим для системы координат « 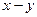», вращающейся синхронно с потокосцеплением ротора ( 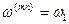) и ориентированной по его направлению.

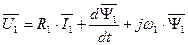. (120)

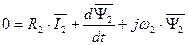. (121)

Представим обобщенные вектора тока, напряжения и потокосцепления в уравнениях (120) и (121) комплексными векторами, записанными в алгебраической форме в системе координат « ».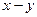

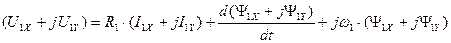. (122)

. (123)

Раскрывая скобки, преобразуя алгебраические выражения и приравнивая действительные и мнимые части в правой и левой частях выражений (122) и (123) получим четыре уравнения для цепей статора и ротора.

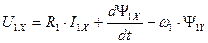. (124)

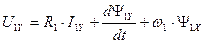. (125)

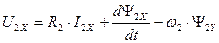. (126)

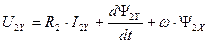. (127)

Для вычисления модуля электромагнитного момента АД « 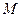» используются векторы потокосцепления статора 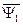и тока ротора .

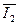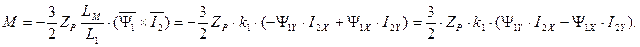Подставим в выражение для электромагнитного момента АД выражение для тока статора .

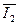Выражение для тока статора 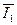получено из выражения:

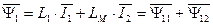. (128)

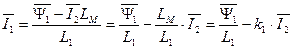, (129)

где 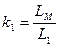. (129а)

Для записи уравнений модели АД применим обобщенные векторы 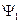и 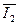в системе координат « 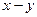». Сначала рассмотрим уравнение для статора.

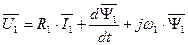. (130)

Подставим выражение (129) в уравнение (130) и применим операторную форму записи, заменив символы 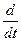на символы 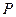. Получим

.

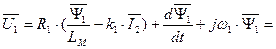
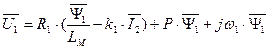После преобразования получим в операторной форме уравнение для статора.

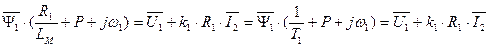. (131)

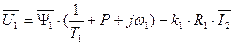, (132)

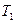– электромагнитная постоянная времени статора.

Получив уравнение для статора (132), рассмотрим уравнение для ротора.

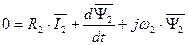. (133)

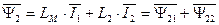. (134)

Преобразуем выражение (133) и применим операторную форму записи, заменив символы 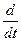на символы 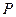. После преобразования получим

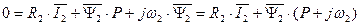. (135)

Преобразуем выражение (134). После преобразования получим

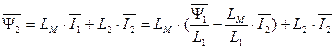. (136)

Подставим в уравнение (135) 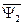из выражения (136). Получим

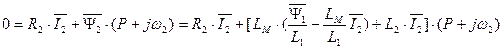. (137)

Преобразуем выражение (137). После преобразования получим

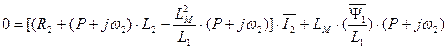. (138)

Разделим правую и левую части выражения (138) на 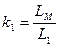. После преобразования получим в операторную форме уравнение для ротора.

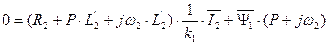, (139)

где 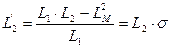; (140)

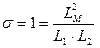- коэффициент рассеяния.

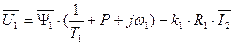. (141)

В результате проведенных преобразований вместо четырех уравнений с четырьмя неизвестными обобщенными векторами получили два уравнения (139) и (141) с двумя неизвестным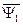и и 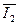, с помощью которых можно вычислить модуль электромагнитного момента АД « ».

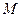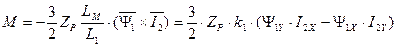. (142)

Вычитая из уравнения (141) уравнение (139), можно понизить порядок системы уравнений модели АД. В результате проведенных преобразований получим

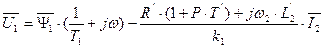, (143)

где 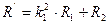- расчетный параметр;

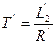- расчетная постоянная времени.