Преобразование «обобщенных» векторов потокосцеплений статора и ротора АД при записи в другой системе координат

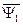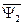В выражениях (47) и (48) для потокосцеплений и векторы тока статора и ротора записаны в различных системах координат. Так, в выражении для потокосцепления 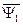ток статора записан в неподвижной системе координат « 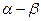», связанной со статором, а ток ротора во вращающейся системе координат « 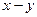», связанной с ротором (смещенной на текущий угол « 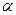» ). Полная запись выражения для потокосцепления 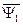с учетом индексов систем координат выглядит следующим образом.

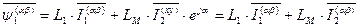. (69)

Если обе части выражения (69) умножить на оператор поворота 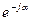, то получим:

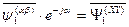. (70)

Запишем выражение (70) в развернутом виде с учетом выражения (51).

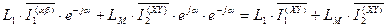. (71)

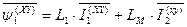. (72)

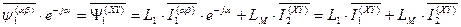. (73)

Тогда окончательно потокосцепления статора с учетом всех токов АД и независимо от выбранной системы координат можно представить в виде

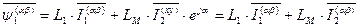. (74)

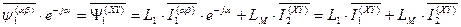. (75)

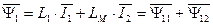. (76)

По аналогии также можно записать потокосцепления ротора с учетом всех токов АД независимо от выбранной системы координат.

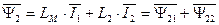. (77)

В уравнениях (76) и (77) все коэффициенты являются постоянными величинами и не зависят от взаимного расположения обмоток статора и ротора, т.к токи статора и ротора записаны в одной и той же системе координат.

Из выражений следует, что потокосцепления статора и ротора раскладываются на составляющие, обусловленные собственным током ( 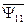и 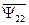) и током другой части АД ( 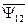и ).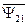

Пользуясь тем, что сумма токов статора и ротора образует ток намагничивания АД (см. рис. 12), т.е. , потокосцепления статора 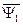и ротора 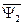можно также представить через потокосцепление основного магнитного потока 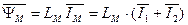и потокосцепления рассеяния статора 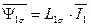и ротора .

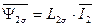Рис. 12. Схема замещения АД

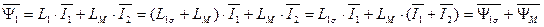. (78)

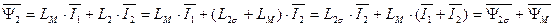. (79)