Преобразование уравнений статора и ротора для записи в общей системе координат

Уравнения для цепи статора и ротора с применением обобщенных векторов тока, напряжения и потокосцепления имеют следующий вид.

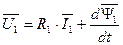. (80)

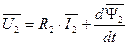. (81)

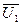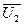Уравнения для и записаны в разных системах координат. Уравнение для статорной цепи 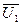записано в неподвижной системе координат с осями 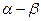. Уравнение для роторной цепи 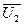записано во вращающейся системе координат с осями 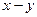. Для перевода и записи уравнения для роторной цепи 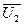в неподвижной системе координат « 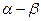» умножим обе его части на оператор поворота 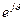. Умножение уравнения для 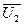на оператор поворота 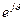осуществляет поворот системы координат « 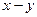» на текущий угол поворота 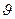. Представим в производной ( 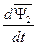) вектор потокосцепления ротора ( 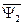) в системе координат « 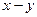» как 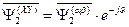. (82)

После преобразований с учетом выражения (82), опуская индексы координатной системы, получим уравнение ротора в векторной форме в системе координат статора « ».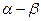

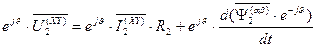. (83)

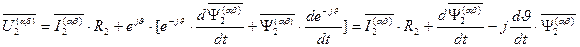. (84)

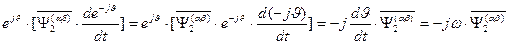. (85)

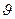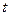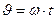Если угол поворота изменяется прямо пропорционально времени , т.е , то 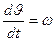– текущая скорость вращения ротора.

Таким образом, уравнение ротора в векторной форме в неподвижной системе координат статора « 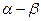» выглядит так.

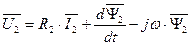. (86)