Обобщенная электрическая машина (ОЭМ)
Уравнениям (96), (97)), (103) и (104) соответствует электрическая машина с одной парой полюсов и двумя обмотками на статоре и роторе, расположенными на взаимно-перпендикулярных осях и неподвижными друг относительно друга. Такая электрическая машина называется обобщенной (ОЭМ).
Обобщенная электрическая машина (ОЭМ) характеризуется следующими свойствами:
1. ОЭМ симметрична и имеет равномерный воздушный зазор;
2. магнитопровод машины (ОЭМ) ненасыщен;
3. МДС обмоток имеет синусоидальное распределение по рабочему зазору.

Рис. 13. Модель обобщенной электрической машины (ОЭМ) при записи уравнения для статора в системе координат « 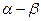 » и уравнения для ротора в системе координат «
» и уравнения для ротора в системе координат « 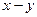 »
»

Рис. 14. Модель обобщенной электрической машины (ОЭМ) при записи уравнения для статора и ротора в системе координат « 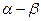 »
»
Модель обобщенной электрической машины (ОЭМ) универсальна и при принятии определенных условий, из нее можно получить все типы электрических машин как частные случаи. Например, при питании обмоток статора от двух источников переменного синусоидального тока, смещенных по фазе на 90° , в рабочем зазоре создается круговое вращающееся магнитное поле.
Если одну из обмоток ротора подключить к источнику постоянного тока, то мы получим модель синхронной машины.
Если обе обмотки ротора замкнуть накоротко, то образуется модель асинхронной короткозамкнутой машины.
Если одну из обмоток статора подключить к источнику постоянного тока, а обмотки ротора подключить к двум источникам переменного синусоидального тока с частотой, равной частоте вращения ротора, и фазовым смещением в 90°, таким образом, чтобы поле ротора вращалось в направлении противоположном направлению вращения его вала, то мы получим модель машины постоянного тока. В этой модели поле ротора формируется источниками питания переменного тока с управляемой частотой, роль которых в реальной машине играет источник постоянного тока и коллектор.
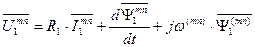 . (105)
. (105)
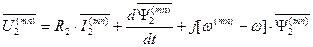 . (106)
. (106)
Эти уравнения соответствуют модели обобщенной электрической машины в системе координат, вращающейся с произвольной угловой частой 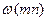 . Уравнения, записанные в системе координат «
. Уравнения, записанные в системе координат « 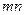 », вращающейся с произвольной угловой частой
», вращающейся с произвольной угловой частой 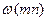 , можно разложить на составляющие, представив векторные величины в виде комплексных чисел.
, можно разложить на составляющие, представив векторные величины в виде комплексных чисел.
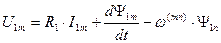 . (107)
. (107)
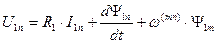 . (108)
. (108)
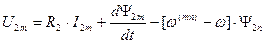 . (109)
. (109)
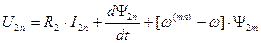 . (110)
. (110)
Из уравнений (107) - (110) следует, что в произвольно вращающейся системе координат ЭДС вращения существует как в статоре, так и в роторе. Наличие ЭДС вращения приводит к появлению перекрестных связей в структуре модели машины, т.к. это слагаемое образуется проекцией потокосцепления на другую ось координат, что существенно затрудняет построение систем управления.
Исключить ЭДС вращения можно надлежащим выбором угловой частоты вращения системы координат, но только либо в уравнениях статора ( 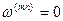 ), либо в уравнениях ротора (
), либо в уравнениях ротора ( 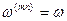 ).
).
Эти уравнения можно представить электрической схемой замещения на рис. 15.

Рис. 15. Электрическая схема замещения по уравнениям АД в произвольно вращающейся системе координат
В короткозамкнутом АД ( 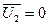 ) эти уравнения принимают вид
) эти уравнения принимают вид
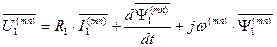 . (111)
. (111)
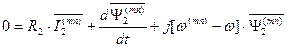 . (112)
. (112)
При этом отсутствие внешнего источника электрической энергии, питающего ротор короткозамкнутого АД, определяет следующее соотношение частот статора и ротора 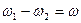 .
.
Дата добавления: 2020-10-25; просмотров: 689;











