Швидкість і прискорення руху
Яка б не була траєкторія руху (прямолінійна або криволінійна), якщо за рівні проміжки часу матеріальна точка проходить рівні ділянки шляху, то такий рух називається рівномірним. Якщо шляхи, пройдені за рівні проміжки часу, не однакові, то рух називають нерівномірним.
Для характеристики руху вводиться поняття вектора середньої швидкості руху.
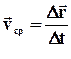 . (1.1)
. (1.1)
У механіці швидкість визначають як вектор, що вказує і швидкість, і напрям руху. У зв'язку з цим, поняття швидкості в механіці пов'язане з уявленням про елементарне переміщення, оскільки кінцеве (неелементарне) переміщення при криволінійному русі не дозволяє визначити напрям руху.
У фізиці найбільший інтерес представляє не середня, а миттєва швидкість, яка визначається як межа, до якої прагне середня швидкість за нескінченно малий проміжок часу Δt :
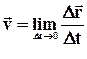 .
.
У математиці таку межу називають похідною і позначають:
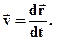 (1.2)
(1.2)
За одиницю швидкості приймають 1 м/с.
Миттєва швидкість 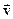 тіла в будь-якій точці криволінійної траєкторії спрямована по дотичній до траєкторії в цій точці. Відмінність між середньою і миттєвою швидкостями показано на рисунку 1.3.
тіла в будь-якій точці криволінійної траєкторії спрямована по дотичній до траєкторії в цій точці. Відмінність між середньою і миттєвою швидкостями показано на рисунку 1.3.
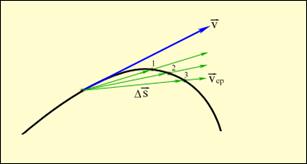
Рисунок 1.3.
Чисельне значення вектора швидкості дорівнює відношенню елемента довжини шляху ds до проміжку часу dt:
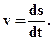 (1.3)
(1.3)
Чисельне значення вектора швидкості дорівнює похідній першого порядку від шляху за часом. Якщо відома довжина шляху як функція часу S=f(t), тоді v=f ′(t).
Коли точка здійснює елементарне переміщення 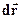 , її координати змінюються на
, її координати змінюються на 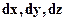 ; ці величини є проекціями елементарного переміщення
; ці величини є проекціями елементарного переміщення 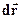 на осі координат. Проекція швидкості на вісь координат (компонент швидкості) є швидкістю переміщення у напрямі цієї осі. Таким чином:
на осі координат. Проекція швидкості на вісь координат (компонент швидкості) є швидкістю переміщення у напрямі цієї осі. Таким чином:
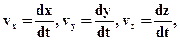 тоді
тоді 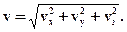
Прискорення
Рух з незмінною швидкістю відбувається досить рідко. В більшості випадків швидкість руху міняється як за величиною, так і по напряму. Зміна швидкості характеризується прискоренням.
При русі тіла по криволінійній траєкторії його швидкість 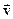 змінюється за величиною і напрямом. Зміна вектора швидкості
змінюється за величиною і напрямом. Зміна вектора швидкості 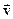 за деякий малий проміжок часу Δt можна задати за допомогою вектора
за деякий малий проміжок часу Δt можна задати за допомогою вектора 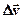 (рис.1.4).
(рис.1.4).
Вектор зміни швидкості 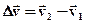 , можна розкласти на дві складові:
, можна розкласти на дві складові:
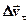 (дотичну або тангенціальну складова), спрямовану уздовж вектора
(дотичну або тангенціальну складова), спрямовану уздовж вектора 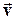 , і
, і 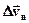 (нормальну складову), спрямовану перпендикулярно вектору
(нормальну складову), спрямовану перпендикулярно вектору 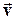 .
.
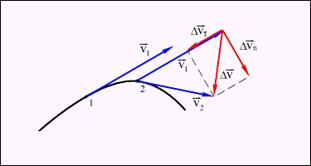 |
Рисунок 1.4.
Миттєвим прискоренням (чи просто прискоренням) 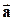 тіла називають межу відношення малої зміни швидкості
тіла називають межу відношення малої зміни швидкості 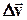 до малого проміжку часу Δt, впродовж якого відбувалася зміна швидкості, або похідну від швидкості за часом:
до малого проміжку часу Δt, впродовж якого відбувалася зміна швидкості, або похідну від швидкості за часом:
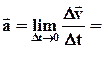
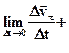
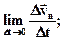
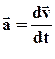 . (1.4)
. (1.4)
Таким чином, прискорення являється векторною величиною, і дорівнює першій похідній швидкості за часом. За одиницю прискорення приймають 1м/с2.
Напрям вектора прискорення 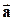 у разі криволінійного руху не співпадає з напрямом вектора швидкості
у разі криволінійного руху не співпадає з напрямом вектора швидкості 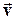 , тому при дослідженні механічного руху можна розкласти вектор прискорення
, тому при дослідженні механічного руху можна розкласти вектор прискорення 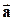 два складових вектори: на прискорення по дотичній до траєкторії цієї точки (тангенціальне
два складових вектори: на прискорення по дотичній до траєкторії цієї точки (тангенціальне 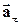 ) і прискорення по головній нормалі (нормальне прискорення
) і прискорення по головній нормалі (нормальне прискорення 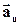 )(рис.1. 5).
)(рис.1. 5).
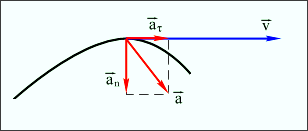
Рисунок 1.5.
Дотичне (тангенціальне) прискорення вказує, як швидко змінюється швидкість тіла по модулю:
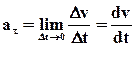 . (1.5)
. (1.5)
Вектор 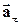 спрямований по дотичній до траєкторії і співпадає з напрямом вектора швидкості, якщо рух прискорений, при уповільненому русі вектор
спрямований по дотичній до траєкторії і співпадає з напрямом вектора швидкості, якщо рух прискорений, при уповільненому русі вектор 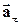 і
і 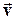 спрямовані протилежно.
спрямовані протилежно.
Нормальне прискорення вказує, як швидко швидкість тіла змінюється по напряму. Вектор нормального прискорення 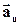 направлений завжди перпендикулярно швидкості.
направлений завжди перпендикулярно швидкості.
Криволінійний рух можна представити як рух по дугах кіл (рис. 1.6).
Вектор нормального прискорення спрямований по радіусу до центру кола. Його називають ще доцентровим прискоренням . Модуль доцентрового прискорення пов'язаний з лінійною швидкістю співвідношенням:
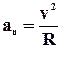 . (1.6)
. (1.6)
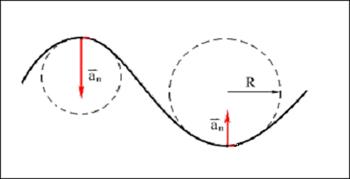
Рисунок 1. 6.
Таким чином, при русі матеріальної точки по криволінійній траєкторії вектор прискорення геометрично складається з прискорення тангенціального, спрямованого по дотичній до траєкторії руху і прискорення нормального, спрямованого по головній нормалі до центру кола.
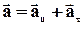 .
.
Модуль вектора прискорення визначається по теоремі Піфагора
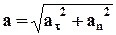 . (1.7)
. (1.7)
Дата добавления: 2020-10-25; просмотров: 1175;











