Приклад розв’язку задачі.

Точка рухається по осі Х згідно із законом х = 2 + 5t +2 t², де t в секундах, а х - в метрах. Визначити координату, швидкість і прискорення цієї точки у момент часу t= 2с.

1. Для знаходження координати точки у момент часу 2 с потрібно в рівняння рух підставити цей момент часу.

Х(2) = 2 + 5·2 +2 ·2²=20 м.

2. Для знаходження швидкості точки у момент часу 2с необхідно отримати рівняння швидкості (залежність швидкості руху від часу) і підставити в це рівняння момент часи 2 с.

Так, як рух відбувається уздовж осі Х V=V_X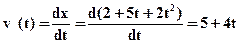

V(t)=5+4·2=13 м/с.

3. Для знаходження прискорення точки у момент часу 2с необхідно отримати рівняння прискорення (залежність прискорення руху від часу) і підставити в це рівняння момент часи 2 с.

Так, як рух прямолінійний повне прискорення дорівнює тангенціальному прискоренню

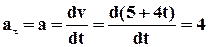м/с².

Рух тіл з прискоренням вільного падіння

Вільним падінням тіл називають падіння тіл на Землю у відсутність опору повітря (у порожнечі). У кінці XVI століття знаменитий італійський вчений Галілео Галілей дослідним шляхом встановив, що у відсутність опору повітря усі тіла падають на Землю рівноприскорено, і що в даній точці Землі прискорення усіх тіл при падінні одне і те ж. До цього впродовж майже двох тисяч років, починаючи з Аристотеля, в науці було прийнято вважати, що важкі тіла падають на Землю швидше за легких.

Рух по колу

Рух тіла по колу є частковим випадком криволінійного руху. При русі точки по колу зручно вибрати в якості координати кут φ, на який обертається радіус, що вказує миттєве положення точки. Кінематичне рівняння обертання виражає кут повороту як деяку функцію часу t φ =f(t). Кут повороту у фізиці вимірюється в радіанах (Рад).

Кутовою швидкістю ω тіл в даній точці кругової траєкторії називають межу (при Δt→ 0) відношення малого кутового переміщення Δφ до малого проміжку часу Δt (похідну кута повороту від часу) :

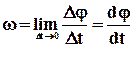. (1.8)

Коли при обертанні кут повороту змінюється пропорційно часу (що має місце при рівномірному русі), кутова швидкість постійна.

Для характеристики рівномірного руху точки по колу введено дві спеціальні величини: частота і період обертання. Час, впродовж якого, тіло здійснює повний оберт, називається періодом обертання. Період позначається буквою Т, і вимірюється в секундах. Частотою обертання називають число оборотів N матеріальної точки навколо центру обертання за секунду. Частота позначається грецькою буквою ν(ню) і вимірюється в герцах 1Гц=1/с.

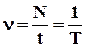. (1.9)

Кутову швидкість зручно виражати через частоту і період обертання

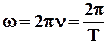. (1.10)

Кутова швидкість вимірюється в рад/с.

Знайдемо зв'язок між лінійними і кутовими параметрами руху. (рис. 1.7).

Довжина дуги пов'язана з кутом повороту співвідношенням Δl = RΔφ.

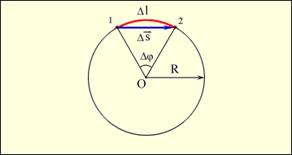
v = ωR

Рисунок 1.7.

Розділивши обидві частини цього рівняння на час отримаємо:

v=ωR.

У разі нерівномірного обертання можна записати:

dl=Rdφ.

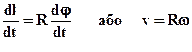. (1.11)

При нерівномірному обертанні кутова швидкість змінюється з часом. Швидкість зміни кутової швидкості характеризують фізичною величиною, яку називають кутовим прискоренням. Якщо за нескінченно малий проміжок часу dt кутова швидкість змінилася на dω, то під кутовим прискоренням розуміють відношення

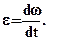(1.12)

Одиницею кутового прискорення являється рад/с².

Лінійне прискорення при обертанні, як і при будь-якому криволінійному русі, можна розкласти на дві складові – тангенціальне і нормальне прискорення.

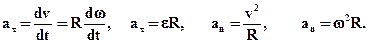(1.13)

Для повної характеристики обертального руху тіла має бути вказане не лише чисельне значення кутової швидкості і кутового прискорення, але і вісь обертання, а також напрям обертання навколо цієї осі. Тому кутову швидкість представляють як вектор, спрямований по осі обертання (рис 1.8). Напрям цього вектора уздовж осі визначається правилом правого гвинта. Кутове прискорення також являється векторною величиною. Вектор кутового прискорення ε спрямований по осі обертання і в ту ж сторону, що і вектор кутової швидкості ω, коли обертання прискорене, і убік протилежний ω, коли обертання сповільнене.

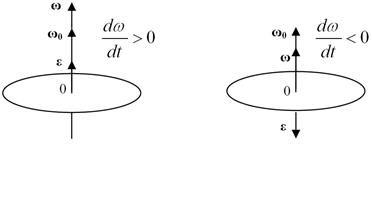
Рисунок 1.8.