Теорема о взаимности работ. Теорема о взаимности перемещений

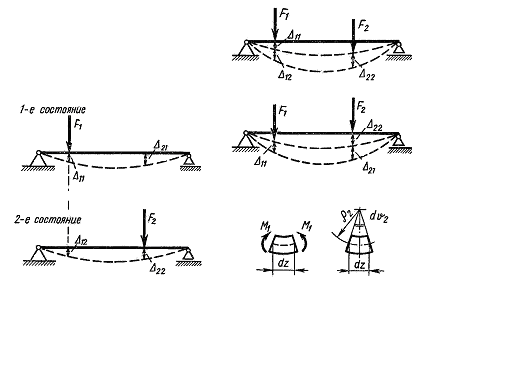
Докажем теорему, имеющую важные приложения, а именно теорему о взаимности работ. Для этого рассмотрим какую-нибудь линейно-деформируемую систему в двух различных, состояниях, отвечающих двум различным нагрузкам (рис. 5.11) Для простоты выкладок рассмотрим простую балку, нагруженную в обоих состояниях самой простой нагрузкой (по одной сосредоточенной силе). Нагрузка, внутренние усилия и деформации, соответствующие этим состояниям, отмечены индексами 1 и 2.

На рис. 5.11 а изображено первое состояние системы, а на рис. 5.11 б - второе.

Перемещение по направлению нагрузки в первом состоянии от этой же нагрузки обозначено ∆₁₁. Перемещение по направлению нагрузки второго состояния, вызванное действием нагрузки первого состояния, обозначено ∆₂₁. Обозначения перемещений второго состояния приведены на рис. 5.11 б. Перемещения, содержащие в своем обозначении два одинаковых индекса, как, например,∆₁₁ ,∆₂₂, называются главными, а перемещения вида ∆ ₂₁, ∆ ₁₂ и т. д. - побочными.Докажем теперь теорему о взаимности работ, а именно: работа внешних сил первого состояния на перемещениях второго состояния равна работе сил второго состояния на перемещениях, вызванных силами первого состояния.

а)     б)

а)   б)

Рис. 5.11. Рис. 5.12.

Для доказательства теоремы нагрузим балку силами F₁ и F₂ , прикладывая их в разной последовательности.

1. Вначале приложим нагрузку F₁, а затем к деформированной балке приложим силу F₂ (рис. 5.12 а).

Подсчитаем работу, произведенную при этом внешними силами.

Работа, произведенная силой F₁ на собственном перемещении ∆₁₁ вызванном этой силой, 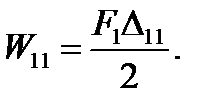Работа, произведенная силой F₂ на собственном перемещении ∆₂₂,

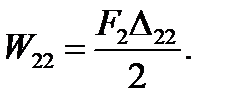
Дополнительная работа силы F₁на перемещении ∆₁₂, вызванном силой F₂,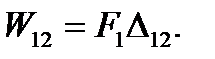

Обращаем внимание на то, что при вычислении W₁₂ множитель 1/2 отсутствует, так как сила F на перемещении ∆₁₂ совершает работу, оставаясь постоянной.

Полная работа, совершенная внешними силами при первом способе (последовательности) нагружения,

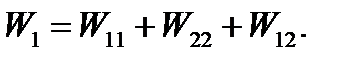(5.24)

Работа W₁₂, фактически совершаемая силой на перемещениях, вызванных другой силой (силами), называетсядополнительной работой. Однако эта работа может и не совершаться, а может рассматриваться лишь как возможная, т. е. такая, которая будет произведена, если нагрузить систему сразу обеими нагрузками. Такую работу называютвиртуальной (возможной) работой.

При дальнейших выкладках не будем делать различия между дополнительной и виртуальной работой.

2. Нагрузим теперь балку в другой последовательности: вначале приложим силу F₂, а затем силу F₁ (рис. 5.12 б). Работа, произведенная силой F₂ на собственном перемещении ∆₂₂,

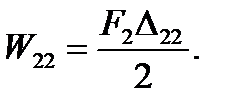(5.25)

Работа, произведенная силой F₁ на собственном перемещении ∆₁₁,

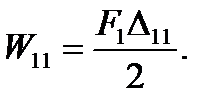(5.26)

Работа, произведенная силой F₂ на перемещении ∆₂₁ ,

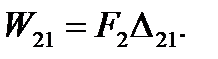(5.27)

Полная работа при втором способе нагружения

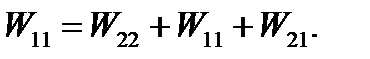(5.28)

Однако работа сил не зависит от порядка их приложения. Следовательно, W₁ = W₁₁, откуда получим

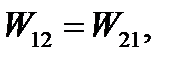(5.29)

или для рассматриваемого случая

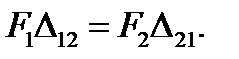(5.30)

Этим доказана сформулированная выше теорема о взаимности виртуальных работ внешних сил. Мы доказали ее на примере сосредоточенных внешних нагрузок. Однако теорема остается справедливой и для любой внешней нагрузки: сосредоточенной, распределенной, внешних моментов. Следует только иметь в виду, что работа моментов вычисляется уже не на линейных, а на угловых перемещениях.

Аналогичным образом может быть доказана также взаимность виртуальной работы внутренних сил:

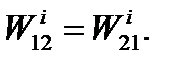(5.31)

Используя закон сохранения энергии, можно показать, что дополнительная работа внешних сил равна по абсолютному значению дополнительной работе внутренних сил: 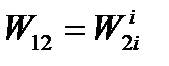и

И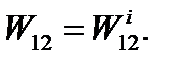з этого следует также, что

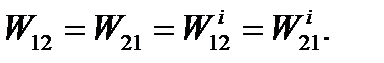(5.32)

Эти соотношения будут использованы далее для обоснования общего метода определения перемещений (метода Мора). Из теоремы о взаимности работ как частный случай следует другая важнаятеорема о взаимности перемещений.

Принимая F₁ = F₂ =1, получим

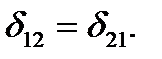(5.33)

Здесь перемещения, вызываемые силами, равными единице (единичными силами), обозначают 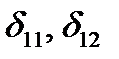и т. д.

Перемещение точки приложения единичной силы по ее направлению, вызванное второй единичной силой, равно перемещению точки приложения второй единичной силы по направлению последней, вызванному действием первой единичной силы.