Определение перемещений методом Мора

Рассмотрим теперь общий метод определения перемещений, пригодный для любой линейно-деформируемой системы при любой нагрузке. Этот метод предложен выдающимся немецким ученым О. Мором.

Пусть, например, требуется определить вертикальное перемещение точки В балки, представленной на рис. 5.13 а. Заданное (грузовое) состояние обозначим f. Выберем вспомогательное состояние той же балки с единичной (безразмерной) силой, действующей в точке В в направлении искомого перемещения. Вспомогательное состояние обозначим k (рис. 5.13 б).

Определим работу внешних и внутренних сил вспомогательного состояния на перемещениях, вызванных действием сил грузового состояния.

Работа внешних сил равна произведению единичной силы на искомое перемещение :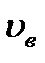

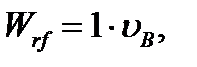(5.34)

а работа внутренних сил равна интегралу:

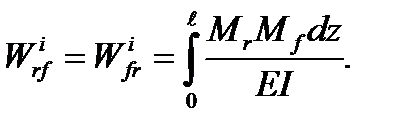(5.35)

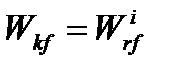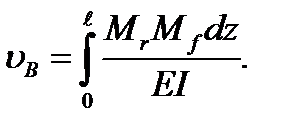Но или (5.36)

a)     б)

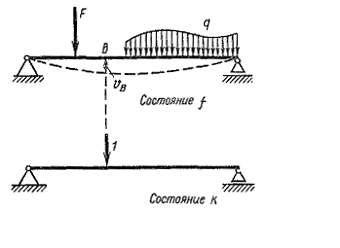
Рис. 5.13

Эта формула и естьформула Мора (интеграл Мора), которая дает возможность определить перемещение в любой точке линейно-деформируемой системы.

В этой формуле подынтегральное произведение M_kM_f положительно, если оба изгибающих момента имеют одинаковый знак, и отрицательно, если M_k и M_f имеют разные знаки.

Если бы мы определяли угловое перемещение в точке В, то в состоянии k следовало бы приложить в точке В момент, равный единице (без размерности).

Обозначая Δ любое перемещение (линейное или угловое), формулу (интеграл) Мора напишем в виде

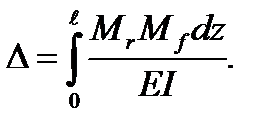(5.37)

В общем случае аналитические выражения M_k, M_f, может быть различным на разных участках балки или вообще упругой системы. Поэтому следует пользоваться более общей формулой

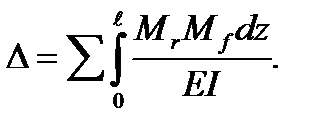(5.38)

Если стержни систем работают на изгиб и растяжение, то следует пользоваться формулой

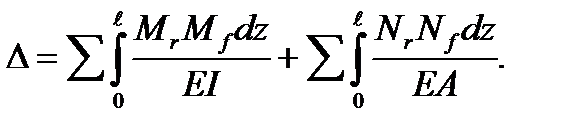(5.39)

В частном случае, когда стержни работают только на растяжение или сжатие (фермы), формула для определения перемещений имеет вид

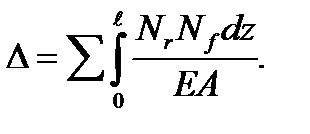(5.40)

В этой формуле произведение N_k N_f, положительно, если оба усилия растягивающие или сжимающие.

При расчете рам, когда стержни работают одновременно и на изгиб, и на растяжение (сжатие), в обычных случаях, как показывают сравнительные расчеты, перемещения можно определять, учитывая лишь изгибающие моменты, так как влияние продольных сил весьма мало. По тем же соображениям, в обычных случаях можно не учитывать влияния поперечных сил.

Если состояния f и k одинаковы, то получим:

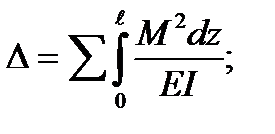
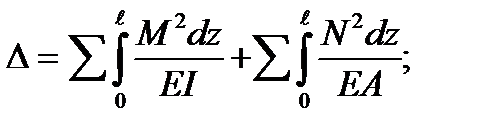(5.41)

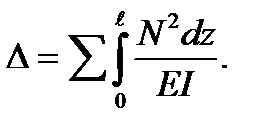
ТЕОРИИ ПРОЧНОСТИ