Определение нормальных напряжений

При чистом плоском (простом) изгибе в поперечных сечениях балки возникают только изгибающие моменты в плоскости, проходящей через одну из главных осей поперечного сечения балки. Изгибающий момент представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению.

Чтобы установить закон распределения и значения внутренних сил, возникающих в поперечном сечении балки, уравнений статики недостаточно. Необходимо использовать условия деформации балки.

Если подвергнуть чистому плоскому изгибу балку (образец) с нанесенной на ее поверхности сеткой, то обнаружится следующее (рис. 5.9):

1) линии 1-1 и 2-2 на поверхности балки после деформации повернутся на некоторый угол du, оставаясь прямыми. Можно полагать, что и поперечные сечения балки плоские до деформации, останутся плоскими и после деформации (гипотеза плоских сечений).

Расчеты, основанные на таком предположении, согласуются с опытом. Поскольку прямоугольная сетка остается прямоугольной и после деформации, можно принять, что касательные напряжения в поперечном сечении равны нулю; волокно ab на выпуклой стороне балки удлиняется, что свидетельствует о растяжении этого волокна, а волокно ef укорачивается, что свидетельствует о его сжатии. Длина же волокна c,d останется без изменения, что свидетельствует о том, что это волокно не испытывает ни растяжения, ни сжатия.

Слой балки (на уровне волокна cd), не испытывающий при изгибе ни растяжения, ни сжатия, называетсянейтральным слоем. Линия пересечения нейтрального слоя с плоскостью поперечного сечения балки (рис. 5.10 а) называетсянейтральной осью (линией). Пересечение силовой плоскости с плоскостью поперечного сечения называется силовой линией.

Из рассмотренных результатов опытов следует, что волокна балки деформируются различно: большие деформации испытывают волокна, более удаленые от нейтрального слоя. Покажем, что по высоте сечения балки деформации изменяются по линейному закону (рис. 5.9). Действительно, отрезок b'b" представляет полное удлинение волокна ab, длина которого до деформации равна длине волокна cd, принадлежащего нейтральному слою (см. рис. 5.9), Относительное удлинение этого волокна

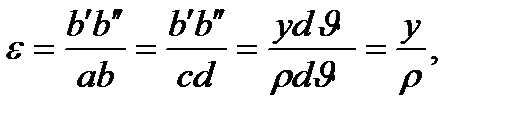(5.10)

где ρ - радиус кривизны нейтрального слоя балки (значение r пока неизвестно); у - расстояние от нейтральной оси до рассматриваемого волокна.

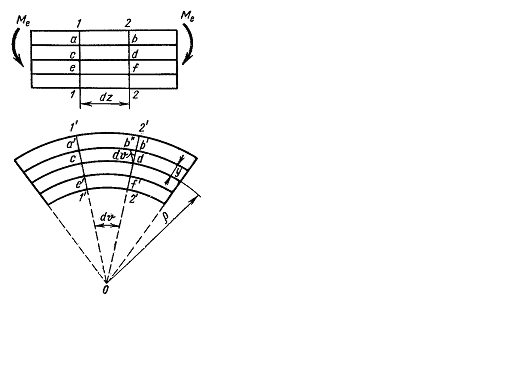
Рис. 5.9

Волокна балки не оказывают давления друг на друга, т. е. напряжения в направлении, перпендикулярном оси балки, равны нулю. Следовательно, каждое волокно испытывает одноосное растяжение или сжатие. Тогда по закону Гука для одноосного напряженного состояния получим

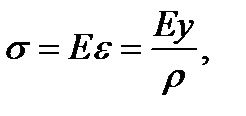(5.11)

т,е. нормальные напряжения изменяются по высоте поперечного сечения балки пропорционально расстоянию от нейтральной оси.Наибольшие напряжения будут у верхнего и нижнего краев сечения. Эпюра 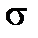показана на рис. 5.10 а. Растягивающие напряжения считаем положительными.

а) б)

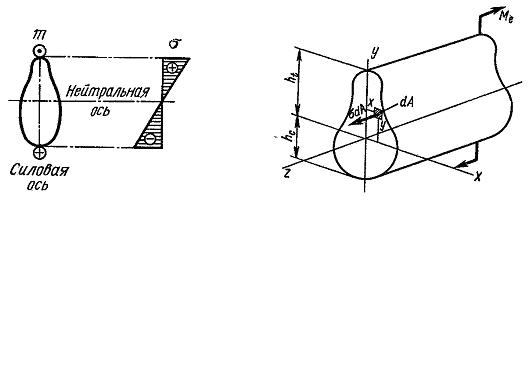
Рис. 5.10.

Установив закон распределения напряжений, можно определить и их значение из уравнений равновесия. Рассмотрим равновесие части балки, находящейся под действием внешнего момента М_е и внутренних сил, возникающих в проведенном поперечном сечении (рис. 5.10 б). При равновесии этой части балки должны соблюдаться шесть уравнений равновесия: равенство нулю суммы проекций действующих сил на три оси координат и равенство нулю трех сумм моментов относительно осей х, у, z.

1. Приравниваем нулю сумму проекций на ось у: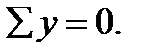

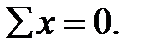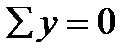2. То же самое - на ось х: Но и 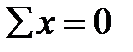обращаются в тождества, так как внутренние силы σdA перпендикулярны этим осям.

3. Приравниваем нулю сумму проекций на ось z:

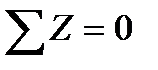или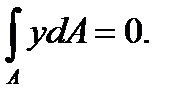

получаем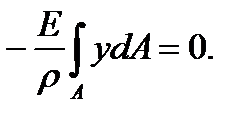

Но 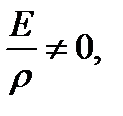так как r ¹ ¥, ибо рассматривается изогнутая балка.

Следовательно,

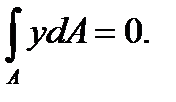
Этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной оси. Он равен нулю, и, следовательно,нейтральная ось при изгибе проходит через центр тяжести сечения.

4. Уравнение 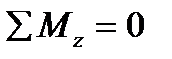обращается в тождество, так как внутренние усилия параллельны оси z.

5. Уравнение 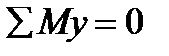дает 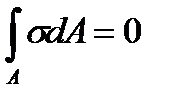. Используя формулу (5.11), получаем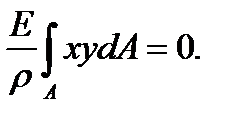

Но 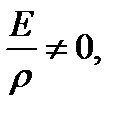следовательно, 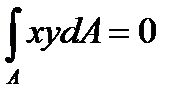. Интеграл 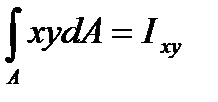представляет собой центробежный момент инерции сечения относительно осей х и у. Так как он равен нулю, то оси х и у должны быть главными осями сечения и момент M_e должен лежать в плоскости, проходящей через одну из главных осей, что и выполняется при плоском изгибе. Из этого условия следует также, чтосиловая линия и нейтральная ось (нулевая линия) взаимно перпендикулярны.

6. Приравниваем нулю сумму моментов сил относительно оси х:

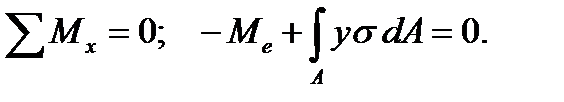
Используя формулу (5.11), получаем 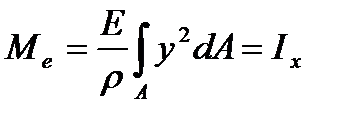, а .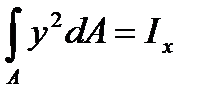

Интеграл J_x представляет собой момент инерции сечения относительно нейтральной оси х. На отсеченную часть балки может действовать не одна внешняя пара, а несколько, а также любая другая нагрузка. В этом случае уравнение равновесия ∑M_x = 0 содержит алгебраическую сумму моментов от всех этих сил, равную изгибающему моменту в поперечном сечении - М. Имея в виду сказанное, последнее соотношение представим в виде

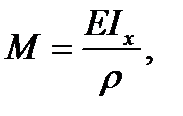(5.12)

откуда

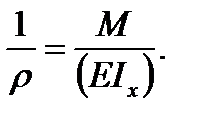(5.13)

Величина 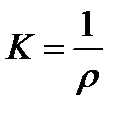представляет собойкривизну нейтрального слоя балки.

Несколько выше было показано, что нейтральная линия поперечного сечения проходит через его центр тяжести. Следовательно, ось (продольная ось) балки, являющаяся геометрическим местом центров тяжести ее поперечных сечений, расположена в нейтральном слое. Таким образом, получаем, что выражение (5.13) определяет кривизну оси балки.

Итак, кривизна оси балки при изгибе пропорциональна изгибающему моменту и обратно пропорциональна величине EI_x, называемой жесткостью балки.

Подставляя найденное значение 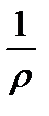в (5.11), получим важную формулу,

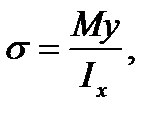(5.14)

позволяющую определить нормальное напряжение в любой точке поперечного сечения балки.

Формула (5.14) выведена для чистого изгиба.

При поперечном изгибе в поперечных сечениях балки возникают и нормальные, и касательные напряжения.

Возникновение касательных напряжений сопровождается появлением деформаций сдвига, в результате чего поперечные сечения балки перестают быть плоскими. Кроме того, при поперечном изгибе возникают напряжения в продольных сечениях балки, т. е. имеет место надавливание волокон друг на друга.

Более детальные исследования показывают, что, несмотря на это, формула (5.14) дает вполне надежные результаты и при поперечном изгибе.