Одночастотные вынужденные колебания. Частотные характеристики
Исследование вынужденных колебаний нелинейных систем представляет собой в общем сложную задачу в связи с отсутствием суперпозиции отдельных решений, а также существенным изменением поведения системы в зависимости от размера амплитуды колебаний, с наличием не единственного установившегося режима и возможностью перескоков с одного режима на другой, с особенностями высших гармоник, субгармоник, комбинационных частот и с многими другими факторами.
В данном разделе мы рассмотрим случай одночастотной системы с частотой внешнего периодического воздействия, и найдем условия их существования.
Рассмотрим нелинейную систему с внешним воздействием (рис. 4.27), заданным в виде
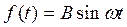 (6.1)
(6.1)
Уравнение динамики системы имеет вид
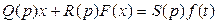 (6.2)
(6.2)
Решение для вынужденных колебаний будем искать приближенно в форме
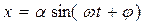 (6.3)
(6.3)
где ω задано, а неизвестными являются амплитуда α и фаза φ.
Произведем гармоническую линеаризацию нелинейности:
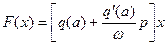 (6.4)
(6.4)
где коэффициенты 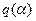 и
и 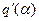 вычисляются для симметричных (нечетных) нелинейностей по прежним формулам (4.11), если в них положить
вычисляются для симметричных (нечетных) нелинейностей по прежним формулам (4.11), если в них положить 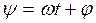 . Для конкретных нелинейностей можно здесь использовать формулы, полученные в разделе 4.2.
. Для конкретных нелинейностей можно здесь использовать формулы, полученные в разделе 4.2.
Подставим (6.1), (6.3) и (6.4) в уравнение системы (6.2):
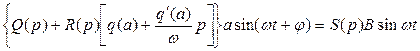 (6.5)
(6.5)
Используем символический метод определения периодического решения, подставив сюда 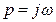 , а вместо
, а вместо 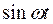 выражение
выражение 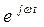 . Тогда получим
. Тогда получим
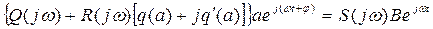
или
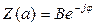 (6.6)
(6.6)
где
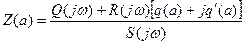 (6.7)
(6.7)
Уравнение (6.6) с двумя неизвестными α и φ можно решить графически, как показано на рис. 6.2. Правая часть (6.6) изображается в виде окружности радиуса B, а левая часть 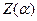 строится как кривая по точкам с переменным параметром α. Точки пересечения окружности с кривой
строится как кривая по точкам с переменным параметром α. Точки пересечения окружности с кривой 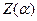 дают решение, причем величина амплитуды вынужденных колебаний определяется в точке пересечения по отметкам на кривой Z, а фаза — по величине угла (рис. 6.2).
дают решение, причем величина амплитуды вынужденных колебаний определяется в точке пересечения по отметкам на кривой Z, а фаза — по величине угла (рис. 6.2).
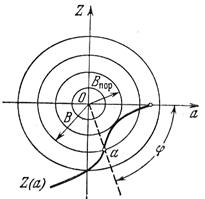
Рис.6.2. Графическое
решение уравнения (6.6)
На рис. 6.2 окружности пересекают кривую только при радиусе, большем некоторого порогового значения 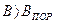 . Следовательно, в этом случае одночастотные вынужденные колебания (6.3) возможны только при достаточно большой амплитуде В, а при меньшей амплитуде В внешнего воздействия будет иметь место сложное движение, включающее в себя и собственную частоту системы.
. Следовательно, в этом случае одночастотные вынужденные колебания (6.3) возможны только при достаточно большой амплитуде В, а при меньшей амплитуде В внешнего воздействия будет иметь место сложное движение, включающее в себя и собственную частоту системы.
Построив серию кривых 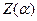 по формуле (6.7) для разных значений частоты внешнего воздействия ω (рис. 6.3), можем построить график зависимости порогового значения В от частоты ω, например, в виде, изображенном на рис. 6.4, где ωα - частота автоколебаний данной системы. Тогда мы получим область значений В и ω, в которой существуют одночастотные вынужденные колебания. Эта область называется областью захватывания. Явление захватывания состоит в том, что при
по формуле (6.7) для разных значений частоты внешнего воздействия ω (рис. 6.3), можем построить график зависимости порогового значения В от частоты ω, например, в виде, изображенном на рис. 6.4, где ωα - частота автоколебаний данной системы. Тогда мы получим область значений В и ω, в которой существуют одночастотные вынужденные колебания. Эта область называется областью захватывания. Явление захватывания состоит в том, что при 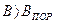 собственные колебания (автоколебания) срываются и система переходит целиком на одночастотные вынужденные колебания с частотой внешнего воздействия. Строго говоря, эти одночастотные вынужденные колебания будут несинусоидальными. В соответствии со свойством фильтра линейной части (раздел 4.1) они для переменной х будут только близки к синусоидальным (6.3).
собственные колебания (автоколебания) срываются и система переходит целиком на одночастотные вынужденные колебания с частотой внешнего воздействия. Строго говоря, эти одночастотные вынужденные колебания будут несинусоидальными. В соответствии со свойством фильтра линейной части (раздел 4.1) они для переменной х будут только близки к синусоидальным (6.3).
На основании рис. 6.3 можно построить зависимости α(ω) и φ(ω), т. е. частотные характеристики замкнутой нелинейной системы по первой гармонике (6.3). В линейных системах частотные характеристики А (ω) и φ(ω) не зависели от размера входной амплитуды и вычислялись для единичной амплитуды на входе. В нелинейной же системе характер частотных характеристик 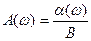 и φ(ω) может существенно зависеть от размера B. Поэтому для разных значений В получается серия частотных характеристик (рис. 6.5) замкнутой системы по первой гармонике.
и φ(ω) может существенно зависеть от размера B. Поэтому для разных значений В получается серия частотных характеристик (рис. 6.5) замкнутой системы по первой гармонике.


Рис. 6.3. Серия кривых 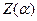 Рис. 6.4. Зависимость
Рис. 6.4. Зависимость
для разных значений порогового значения В
частоты внешнего от частоты ω
воздействия
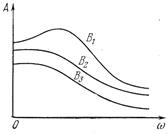
Рис.6.5. Частотные
характеристики для
разных значений В
Пример.6.1. Пусть уравнение системы имеет вид
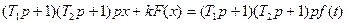
при гистерезисной нелинейности (рис. 6.6) и 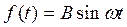 . Тогда в уравнении (6.6), согласно (6.7), будем иметь
. Тогда в уравнении (6.6), согласно (6.7), будем иметь
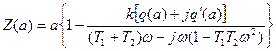
Для заданной частоты 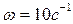 и заданных параметров системы
и заданных параметров системы 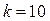 ,
, 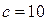 ,
, 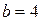 ,
, 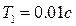 ,
, 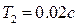 , кривая
, кривая 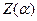 изображена на рис. 6.6, где отмечены значения α. Проведя окружности разных радиусов В, по точкам пересечения определим зависимости
изображена на рис. 6.6, где отмечены значения α. Проведя окружности разных радиусов В, по точкам пересечения определим зависимости 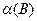 и
и 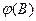 (рис. 6.7) для вынужденных колебаний при данной частоте.
(рис. 6.7) для вынужденных колебаний при данной частоте.


Рис. 6.6.Построение Рис.6.7. Определение
кривой 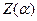 зависимостей
зависимостей 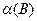 и
и 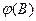
Дата добавления: 2020-10-25; просмотров: 702;











