Функция Ляпунова и ее производная по времени.
Любую дифференцируемую по всем аргументам функцию
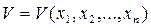 (5.7)
(5.7)
тождественно обращающуюся в нуль при 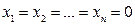 , будем называть функцией Ляпунова, если в ней в качестве величин
, будем называть функцией Ляпунова, если в ней в качестве величин 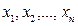 взяты те отклонения переменных системы регулирования в переходном процессе
взяты те отклонения переменных системы регулирования в переходном процессе

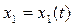
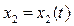
. . . .
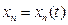
в которых записываются уравнения (5.6) для этой системы. Производная от функции Ляпунова (5.7) по времени будет
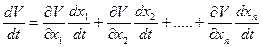
Подставив сюда значения 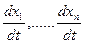 заданных уравнений системы регулирования в общем случае (5.6), получим производную от функции Ляпунова по времени в виде
заданных уравнений системы регулирования в общем случае (5.6), получим производную от функции Ляпунова по времени в виде
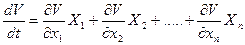 (5.8)
(5.8)
где 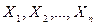 — правые части уравнений (5.6) системы
— правые части уравнений (5.6) системы
автоматического регулирования, представляющие собой
заданные функции от отклонений 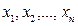 .
.
Следовательно, производная от функции Ляпунова по времени, так же как и сама V, является некоторой функцией отклонений, т. е.
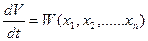 (5.9)
(5.9)
причем эта функция W, так же как и сама V,. тождественно обращается в нуль при 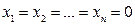 . Поэтому к ней в одинаковой степени можно применять все те же понятия знакоопределенности, знакопостоянства и знакопеременности в некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции V.
. Поэтому к ней в одинаковой степени можно применять все те же понятия знакоопределенности, знакопостоянства и знакопеременности в некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции V.
Здесь шла речь только об уравнениях (нелинейных), в которые не входит в явном виде время t, так как только этот случай будет рассматриваться в дальнейшем. Вообще же метод Ляпунова может применяться и при наличии времени t в явном виде, в частности для уравнений с переменными коэффициентами (линейных и нелинейных).
Базируясь на этих предварительных сведениях, дадим общую формулировку теорем Ляпунова. Теоремы эти годятся для исследования устойчивости систем регулирования не только при малых, но и при больших отклонениях, если для них справедливы исходные уравнения данной системы регулирования. Устойчивость системы при любых больших начальных отклонениях называется коротко устойчивостью в целом.
5.3.2. Теорема Ляпунова об устойчивости нелинейных систем.
Теорема Ляпунова. Если для системы  в области
в области 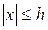 ,
, 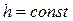 , существует скалярная, дифференцируемая функция состояний системы V(x), такая что:
, существует скалярная, дифференцируемая функция состояний системы V(x), такая что:
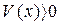 при
при 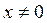 ,
,
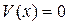 при
при 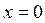 ,
,
и если 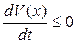 при
при 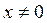 , то система при
, то система при 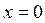 имеет устойчивую точку равновесия,
имеет устойчивую точку равновесия,
если 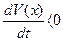 при
при 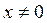 , то система при
, то система при 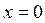 имеет асимптотически-устойчивую точку равновесия.
имеет асимптотически-устойчивую точку равновесия.
Замечание 1. Теорема Ляпунова дает лишь достаточные условия устойчивости точки равновесия.
Замечание 2.
 .
.
Замечание 3. Функцию 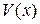 , удовлетворяющую условиям приведенной теоремы, называют функцией Ляпунова.
, удовлетворяющую условиям приведенной теоремы, называют функцией Ляпунова.
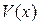 - определенная (положительная или отрицательная) в окрестности начала координат, если она непрерывна, обладает непрерывными первыми производными и имеет в этой окрестности одинаковый знак за исключением точки
- определенная (положительная или отрицательная) в окрестности начала координат, если она непрерывна, обладает непрерывными первыми производными и имеет в этой окрестности одинаковый знак за исключением точки 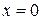 , где она обращается в ноль.
, где она обращается в ноль.
Проиллюстрируем справедливость этой теоремы на наглядных геометрических образах. Для простоты возьмем систему третьего порядка ( 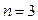 ). Уравнения (5.6) для нее в общем виде будут
). Уравнения (5.6) для нее в общем виде будут

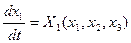
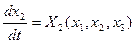 (5.10)
(5.10)
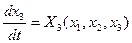
Возьмем знакоопределенную положительную функцию Ляпунова в виде
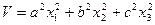 (5.11)
(5.11)
где а, b, с — произвольно заданные вещественные числа. Будем придавать величине V возрастающие постоянные значения: 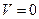 , С1, С2, С3, . . ., что означает
, С1, С2, С3, . . ., что означает
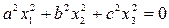
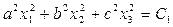
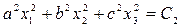
……………………
Первое из этих выражений соответствует одной точке 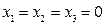 (началу координат фазового пространства), а остальные — поверхностям эллипсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (рис. 5.6).
(началу координат фазового пространства), а остальные — поверхностям эллипсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (рис. 5.6).
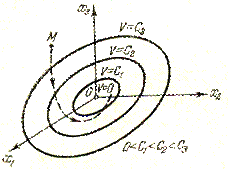
Рис. 5.6. Расположение
эллипсоидов
Возьмем теперь производную от функции Ляпунова по времени. Согласно (5.8) и (5.11) имеем:
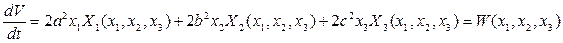 ,
,
где функции 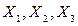 берутся из заданных уравнений системы регулирования (5.11).
берутся из заданных уравнений системы регулирования (5.11).
Если полученная таким путем функция 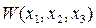 окажется знакоопределенной отрицательной, т.е. если
окажется знакоопределенной отрицательной, т.е. если
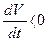 (5.12)
(5.12)
во всех точках исследуемого фазового пространства, кроме одного только начала координат, где
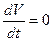 при
при 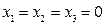 ,
,
то при любых начальных условиях изображающая точка М (рис. 5.6) вследствие (5.12) будет двигаться в сторону уменьшения значения V, т. е. будет пересекать эллипсоиды, изображенные на рис. 5.6, извне внутрь. В результате с течением времени изображающая точка М будет стремиться к началу координат фазового пространства и уже никак не сможет выйти за пределы тех эллипсоидов, в которые она проникла.
Это и означает затухание всех отклонений х1, х2, х3 в переходном процессе с течением времени. Таким образом, установлена устойчивость данной системы регулирования, что иллюстрирует справедливость теоремы для системы третьего порядка (в случае знакоопределенной функции W).
Отсюда вытекает справедливость теоремы и в общем случае. Рассуждения остаются аналогичными, только вместо трех уравнений (5.10) будет n уравнений (5.6). Как и раньше, для любой знакоопределенной положительной функции Ляпунова 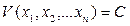 получим некоторые замкнутые поверхности, окружающие начало координат (рис. 5.6), но уже не в обычном трехмерном, а в n-мерном фазовом пространстве (их иногда называют гиперповерхностями). Поэтому, если производная
получим некоторые замкнутые поверхности, окружающие начало координат (рис. 5.6), но уже не в обычном трехмерном, а в n-мерном фазовом пространстве (их иногда называют гиперповерхностями). Поэтому, если производная 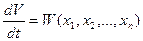 окажется знакоопределенной отрицательной, то траектория изображающей точки М в n-мерном пространстве при любых начальных условиях с течением времени будет пересекать указанные поверхности только извне внутрь, что и свидетельствует об устойчивости данной системы.
окажется знакоопределенной отрицательной, то траектория изображающей точки М в n-мерном пространстве при любых начальных условиях с течением времени будет пересекать указанные поверхности только извне внутрь, что и свидетельствует об устойчивости данной системы.
Если же функция W будет не знакоопределенной, а знакопостоянной, то очевидно, что траектория изображающей точки М не везде будет пересекать поверхности 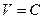 , а может их касаться в тех точках, где W обращается в нуль (помимо начала координат). Но так как во всех других местах фазового пространства функция W имеет один и тот же знак, вследствие чего изображающая точка может идти только извне внутрь поверхности
, а может их касаться в тех точках, где W обращается в нуль (помимо начала координат). Но так как во всех других местах фазового пространства функция W имеет один и тот же знак, вследствие чего изображающая точка может идти только извне внутрь поверхности 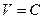 , то при решении задачи остается только проверить, не «застрянет» ли изображающая точка там, где
, то при решении задачи остается только проверить, не «застрянет» ли изображающая точка там, где 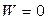 .
.
По поводу сформулированной теоремы Ляпунова об устойчивости системы необходимо сделать следующие два важных замечания.
1. В теореме речь идет о подборе функции Ляпунова 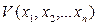 . Вообще говоря, при заданных в форме (5.6) уравнениях системы регулирования можно подобрать несколько различных вариантов функции V, поскольку требуется только знакоопределенность ее и ее производной. Различные варианты функции V, удовлетворяющие теореме, могут дать соответственно различные варианты условий устойчивости для одной и той же системы регулирования. При этом одни из них будут шире, другие уже, последние могут входить в первые, как частный случай и т. д.
. Вообще говоря, при заданных в форме (5.6) уравнениях системы регулирования можно подобрать несколько различных вариантов функции V, поскольку требуется только знакоопределенность ее и ее производной. Различные варианты функции V, удовлетворяющие теореме, могут дать соответственно различные варианты условий устойчивости для одной и той же системы регулирования. При этом одни из них будут шире, другие уже, последние могут входить в первые, как частный случай и т. д.
Поэтому, данная теорема Ляпунова обеспечивает получение достаточных условий устойчивости, которые не всегда будут и необходимыми, т. е. при выполнении условий теоремы система наверняка будет устойчивой, но эти условия могут не охватывать всей области устойчивости системы по параметрам. В самом деле, если выбрана функция V, удовлетворяющая теореме, нет уверенности в том, что нельзя подобрать другой вариант функции V, который бы еще более полно охватывал область устойчивости данной системы.
Геометрически это значит, что, получив определенное семейство поверхностей 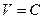 (рис. 5.5) и убедившись, что траектории изображающей точки М приближаются к началу координат, пересекая эти поверхности извне внутрь, нельзя быть уверенным в том, что не существует еще других вариантов траекторий изображающей точки М, которые в отдельных местах могут пересекать данные поверхности изнутри вовне, но все же с течением времени в конце концов неограниченно приближаться к началу координат. Такие траектории будут соответствовать другому семейству поверхностей
(рис. 5.5) и убедившись, что траектории изображающей точки М приближаются к началу координат, пересекая эти поверхности извне внутрь, нельзя быть уверенным в том, что не существует еще других вариантов траекторий изображающей точки М, которые в отдельных местах могут пересекать данные поверхности изнутри вовне, но все же с течением времени в конце концов неограниченно приближаться к началу координат. Такие траектории будут соответствовать другому семейству поверхностей 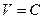 , т. е. другому варианту выбора функции Ляпунова.
, т. е. другому варианту выбора функции Ляпунова.
В ряде технических задач можно вполне удовлетвориться этими достаточными условиями устойчивости. От более или менее удачного подбора функции Ляпунова V будет зависеть большая или меньшая близость полученных достаточных условий устойчивости к необходимым и достаточным, т. е. более или менее полный охват всей области устойчивости данной системы. Существуют, конечно, и такие функции 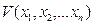 , которые соответствуют всей области устойчивости.
, которые соответствуют всей области устойчивости.
2. К сформулированной выше теореме Ляпунова необходимо добавить, что понятие устойчивости по Ляпунову допускает, чтобы при знакоопределенной функции V производная от нее W была не обязательно знакоопределенной или знакопостоянной, а могла быть и тождественно равна нулю во всем рассматриваемом фазовом пространстве. В этом случае, проводя аналогичные прежним рассуждения, легко убедиться, что изображающая точка М (рис. 5.6) будет оставаться все время на какой-нибудь одной из поверхностей 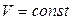 , куда ее забросили начальные условия. В результате система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.
, куда ее забросили начальные условия. В результате система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.
3.Значение функции Ляпунова есть некоторое обобщенное расстояние изображающей точки на траектории от начала координат (точки равновесия). Убывание этого расстояния со временем служит гарантией приближения к точке равновесия. Если, в конце концов, это расстояние станет равным нулю, это означает возвращение траектории движения системы в точку равновесия. Точка равновесия при этом асимптотически устойчива. Если мгновенные возмущения системы 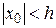 при
при 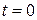 не увеличивают расстояние
не увеличивают расстояние 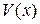 со временем, такая система имеет в нуле устойчивую точку равновесия. Если же в окрестности нуля
со временем, такая система имеет в нуле устойчивую точку равновесия. Если же в окрестности нуля 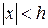 найдется область, в которой
найдется область, в которой 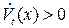 , т. е. расстояние
, т. е. расстояние 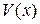 увеличивается со временем, и при некотором
увеличивается со временем, и при некотором 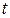
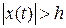 , это означает неустойчивость точки равновесия.
, это означает неустойчивость точки равновесия.
5.3.3. Асимптотическая устойчивость в целом.
Можно предположить, что найдутся системы, для которых окрестностью 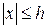 асимптотически устойчивого начала координат является все пространство состояний (т.е.
асимптотически устойчивого начала координат является все пространство состояний (т.е. 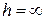 ). В этом случае точка равновесия системы единственна
). В этом случае точка равновесия системы единственна 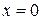 и говорят об асимптотической устойчивости системы в целом. В таких системах траектории всех возмущенных движений заканчиваются в начале координат.
и говорят об асимптотической устойчивости системы в целом. В таких системах траектории всех возмущенных движений заканчиваются в начале координат.
Теорема. Автономная система асимптотически устойчива в целом, если:
1 - начало координат асимптотически устойчиво,
т.е. 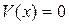 при
при 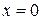 ; и
; и 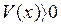 ;
; 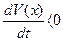 при
при 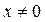 ;
;
2 - 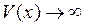 при
при 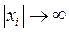 для всех
для всех 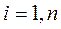 .
.
Итак, требования асимптотической устойчивости системы в целом предполагают возможность построения функции Ляпунова, неограниченно возрастающей при отклонении 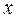 от нуля и увеличении его в любом направлении.
от нуля и увеличении его в любом направлении.
Пример 5.1. Исследуем систему управления курсом самолета (рис. 5.7).
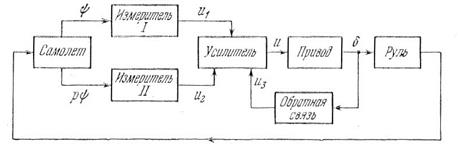
Рис.5.7. Система управления курсом самолета
Уравнение движения самолета в упрощенном виде имеет вид

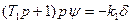
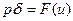 (5.13)
(5.13)
где ψ— угол отклонения оси самолета по курсу,δ — угол отклонения руля, 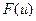 —нелинейная характеристика привода руля (рис. 5.8, а), причем
—нелинейная характеристика привода руля (рис. 5.8, а), причем 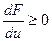 ,
,

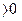 при
при 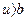
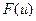
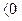 при
при 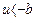 (5.14)
(5.14)
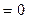 при
при 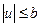
Измерительно-усилительное устройство с обратной связью привода описывается выражением
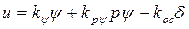 (5.15)
(5.15)
Для перехода к каноническим уравнениям представим уравнение самолета (5.13) в виде
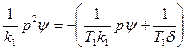
и обозначим

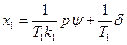
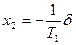 (5.16)
(5.16)
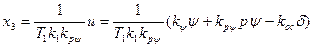
В связи с последним обозначением нелинейная характеристика 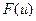 заменится на
заменится на 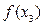 (рис. 5.8,б), где изменится лишь масштаб по оси абсцисс. Поэтому зона нечувствительности вместо b (рис. 5.8,а) будет иметь размер
(рис. 5.8,б), где изменится лишь масштаб по оси абсцисс. Поэтому зона нечувствительности вместо b (рис. 5.8,а) будет иметь размер 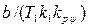 .
.


а) б)
Рис.5.8. Нелинейные характеристики 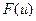 и
и 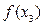
Введем безразмерное время 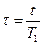 . Тогда система уравнений (5.13), (5.15) преобразуется к каноническому виду
. Тогда система уравнений (5.13), (5.15) преобразуется к каноническому виду

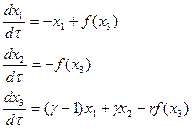 (5.17)
(5.17)
 где
где
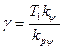
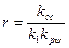 (5.18)
(5.18)
Как видно из уравнений (5.13) — (5.16), установившийся режим полета, устойчивость которого надо исследовать, определяется значениями 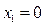 ,
, 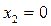 ,
, 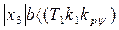 , что иллюстрируется отрезком АВ на рис. 5.9.
, что иллюстрируется отрезком АВ на рис. 5.9.
Рассмотрим отдельно два случая 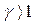 и
и 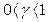 .
.
1. Случай 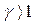 . Функция Ляпунова берется в виде
. Функция Ляпунова берется в виде
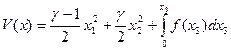 (5.19)
(5.19)
Производная от нее
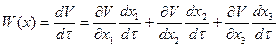
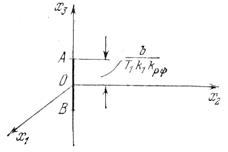
Рис. 5.9. Иллюстрация
установившегося режима
полета
или в силу уравнений системы (5.17) после простых преобразований имеем
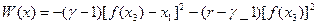
Функция V(x) (5.19) является положительно определенной. Производная же V(х) от нее будет отрицательной знакопостоянной при условии
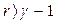 , если
, если 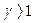 (5.20)
(5.20)
Это и является, следовательно, условием устойчивости системы согласно теореме Ляпунова.
Заметим, что 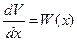 обращается в нуль, когда
обращается в нуль, когда 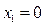 и
и 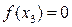 при любом значении x2, т. е. на всей полосе, изображенной на рис. 5.10.
при любом значении x2, т. е. на всей полосе, изображенной на рис. 5.10.
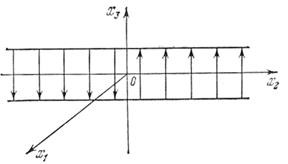
Рис.5.10. Полоса любых
значений x2
Поэтому интересно проверить, не застрянет ли изображающая точка на этой полосе, если фазовая траектория попадет туда. Из уравнений (5.17) на этой полосе имеем

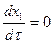
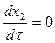
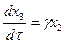
Следовательно, фазовая траектория будет проходить через полосу в направлении, параллельном оси x3, как показано на рис. 5.10, и не застрянет на ней.
2. Случай 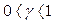 . Функция Ляпунова берется в виде
. Функция Ляпунова берется в виде
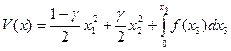
Производная от нее в силу уравнений системы (5.17):
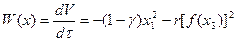
Отсюда условие устойчивости системы, как условие отрицательного знакопостоянства функции W(х), принимает вид
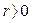 , если
, если 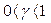 (5.21)
(5.21)
В соответствии с обозначениями (5.19) через исходные параметры системы условия устойчивости (5.20) и (5.21) запишутся в виде соответственно

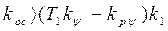 , если
, если 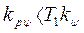 (5.22)
(5.22)
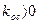 , если
, если 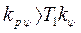
что графически изображено на рис. 5.11, а. Этот результат физически понятен: коэффициент дополнительной обратной связи kос должен быть достаточно большим, если коэффициент интенсивности введения производной от ошибки kpψ взят сравнительно малым. Устойчивость системы не зависит от величины коэффициента обратной связи, если производная введена с достаточно большим коэффициентом.
Согласно (5.21) имеем (при положительных коэффициентах)
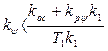
т. е. основной коэффициент усиления автопилота kψ можно увеличить за счет усиления обоих стабилизирующих средств: kос и kpψ, что показано графически на рис. 5.11, б.


а) б)
Рис.5.11. Условия устойчивости системы
Поскольку в условия устойчивости нелинейной системы (5.21) не вошли параметры самой нелинейности, они являются условиями абсолютной устойчивости системы при любой форме однозначной нелинейности, удовлетворяющей лишь условию (5.14).
Дата добавления: 2020-10-25; просмотров: 801;











