Устойчивость. Функция Ляпунова

В теории автоматиче­ского управления и регулирования линейных систем уже давалось общее понятие устойчивости динамической системы по Ляпунову. Напомним ход рассуждений. Запишем уравнения динамики системы n-го порядка при отсутствии возмущающих воздействий в общем нелиней­ном виде в нормальной форме Коши:

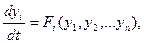
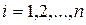(5.1)

Пусть 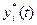обозначает не­который установившийся процесс работы системы, или невозмущенное движение. Отклонение воз­мущенного движения у_i(t), определяемого уравнениями (5.1) при определенных начальных условиях 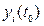, обо­значим через 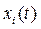, т. е.

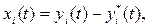
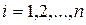(5.2)

Тогда можно написать уравнения возмущенного движе­ния в отклонениях в виде

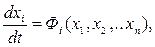
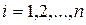(5.3)

при этом невозмущенным движением будет 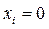. Пере­менные 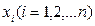являются координатами со­стояния системы.

В общем случае конкретный вид уравнений (5.3) за­висит от вида установившегося процесса 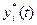, так как эти уравнения получаются из (5.1) подстановкой уравнений (5.2).

Поэтому, исследуя эти уравнения необходимо, вообще говоря, оговаривать, об устойчивости какого установив­шегося режима или невозмущенного движения 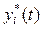идет речь.

Геометрически невозмущенное (установившееся) дви­жение 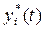системы n-го порядка можно представить условно в виде некоторой интегральной кривой в n-мерном пространстве

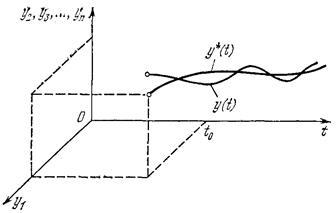
Рис.5.1. Интегральная кривая

в n-мерном пространстве

с добавленной осью времени t (рис. 5.1). Возмущенное движение 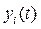, вызванное на­чальным отклонением при 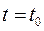, изобразится другой ин­тегральной кривой (рис. 5.1).

В отклонениях 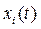, т. е. в пространстве координат состояния системы, эта картина возмущенного движения будет выглядеть, как показано на рис. 5.2.

При этом не­возмущенное движение 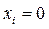изобразится прямой ли­нией, совпадающей с осью t.

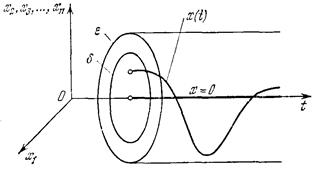
Рис. 5.2. Картина возмущенного

движения

Невозмущенное движение системы 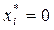называется устойчивым, если, задав «трубку» сколь угодно малого ε-мерного сечения ε (рис. 5.2), можно подобрать в на­чальный момент t₀ такую область начальных условий δ, зависящую от ε, что с увеличением t возмущенное движение 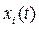не выйдет из заданной трубки ε.

Аналитическое определение понятия устойчивости по Ляпунову формулируется следующим образом.

Невозмущенное движение системы 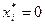называется устойчивым, если при заданном 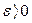сколь бы оно мало ни было, существует такое 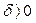, зависящее от ε, что при начальных условиях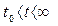

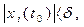
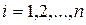(5.4)

в дальнейшем движении ( 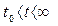) выполняется ус­ловие

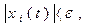
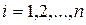(5.5)

Заметим, что в этом аналитическом определении об­ласти ε и δ, в отличие от рис. 5.2, выглядят «прямоуголь­ными» (в n-мерном пространстве), что не имеет прин­ципиального значения.

Невозмущенное движение 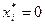будет неустойчивым, если указанное условие не выполняется хотя бы для од­ного из x_i.

Если условия указанного выше определения выполне­ны и имеем 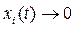при 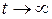, то невозмущенное движение 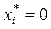называется асимптотически устойчивым. Если же 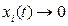при 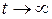после любых начальных отклонений, то система называется устойчивой в целом.

Существует еще понятие абсолютной устойчивости, означающее асимптотическую устойчивость системы в целом при любом характере нелинейности внутри опре­деленного класса нелинейностей.

Различают три характерных типа движения:

1) равновесное состояние (ни одна из координат объекта не изменяется во времени) в про­стран­стве состояний такое движение изображается неподвижной точкой,

2) периодическое движение (объект находится в периодическом движении, если его состоя­ния через равные промежутки времени принимают одни и те же значения), в пространстве со­стояний периодическое движение объекта изображается замкнутой кривой,

3) переходное движение; переход объекта от одного установившегося движения (равновес­ного или периодического) к другому называют переходным движением.

На рис. 5.3 на интервалах времени (t₁,t₂) и (t₃,t₄) объект находится в положении равновесия, а на интервале (t₂,t₃)- в переходном движении.

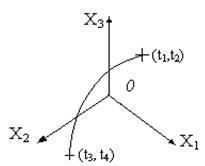
Рис. 5.3. Иллюстрация

переходного движения

При определении понятия устойчивости рассматрива­лись интегральные кривые (рис. 5.1 и 5.2). Если же представить себе не интег­ральную кривую, а фа­зовую траекторию в n-мерном пространстве для системы уравнений (5.3), то в устойчивой системе, согласно опре­делению, она будет иметь вид, изображен­ный на рис. 5.4.

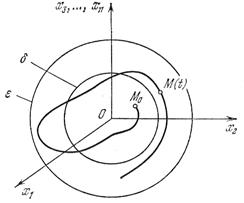
Рис. 5.4. Фа­зовая траектория

для системы уравнений (5.3)