Понятие о знакоопределенных, знакопостоянных и знакопеременных функциях.

Пусть имеется функция нескольких переменных

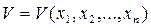
Представим себе n-мерное фазовое пространство, в котором 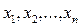являются прямоугольными координатами (это будут, в част­ности, фазовая плоскость при 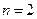и обычное трехмерное пространство при 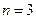). Тогда в каждой точке указанного пространства функция V будет иметь некоторое определенное значение. Нам понадобятся в дальнейшем функции 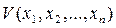, которые обращаются в нуль в начале координат (т. е. при ).

Функция V называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только са­мого начала координат.

Функция V называется зна­копостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Приведем примеры всех трех типов функций V. Пусть 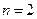и

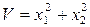
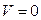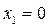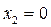Это будет знакоопределенная (положительная) функция, так как только тогда, когда одновременно и , и 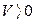при всех вещественных значениях 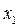и . Аналогично при любом n функция

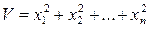
будет знакоопределенной положительной, а 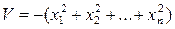— знакоопределенной отрицательной.

Если взять функцию 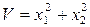при 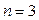, то она уже не будет знако­определенной, так как, оставаясь положительной при любых х₁, х₂ и х₃, она может обращаться в нуль не только при 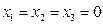, но также и при любом значении х₃, если 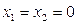(т. е. на всей оси х₃, рис. 5.5, а).

а) б) в)

Рис. 5.5. Примеры всех трех типов функций V

Следовательно, это будет знакопостоянная (положительная) функция.

Наконец, функция 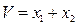будет знакопеременной, так как она положительна для всех точек плоскости справа от прямой 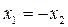(рис. 5.5, б) и отрицательна слева от этой прямой.

Заметим, что в некоторых частных задачах нам понадобится также функция V, которая обращается в нуль не в начале координат, а на заданном конечном отрезке АВ (рис. 5.5, в). Тогда знакоопределенность функции V будет обозначать ее неизменный знак и необращение в нуль в некоторой области вокруг этого отрезка.