Несимметричные автоколебания. Постоянные ошибки

Обратимся к нелинейной системе с внешним воздей­ствием f(t) (рис. 4.27).

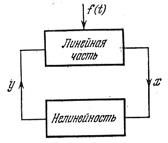
Рис.4.27. Нелинейная система

с внешним воздей­ствием f(t)

Уравнение динамики замк­нутой системы будет иметь вид

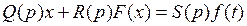, (4.57)

где операторный многочлен S(p) зависит от места приложения внешнего воздействия.

Положим правую часть урав­нения (4.57) постоянной:

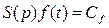(4.58)

Это может быть в двух случаях:

1) внешнее воздей­ствие f(t) постоянно: 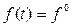, тогда ;

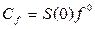2) внешнее воздей­ствие f(t) есть линейная функция с постоянной составляющей: 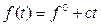, при условии 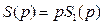, тогда .

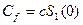Эти случаи соответственно для систем без астатизма и с астатизмом.

Итак, рассмотрим уравнение системы в виде

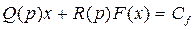(4.59)

В этом случае за счет постоянной правой части уравне­ния появится постоянная составляющая в периодическом решении (несимметричные автоколебания). Поэтому ре­шение ищется в виде (4.15) и (4.16).

Величина 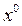характеризует постоянную статическую или скоростную ошибку системы.

Однако несимметричные колебания могут иметь ме­сто и при отсутствии внешнего воздействия, т. е. в си­стеме

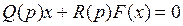(4.60)

если F(x) — несимметричная нелинейность. Это проил­люстрировано на рис. 4.28, где постоянная составляющая F⁰ на выходе нелинейности возникает даже при симмет­ричном входе 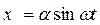. Затем постоянная составляющая, вообще говоря, пройдет и на вход х через линей­ную часть системы и приведет к решению вида (4.15) и (4.16). Следовательно, статическая ошибка в нелинейной систе­ме может иметь место и без внешнего воздействия — за счет несимметрии нелинейности.

Гармоническая линеаризация в случае несимметрич­ных колебаний имеет вид (4.16), т. е.

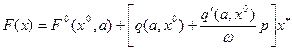(4.61)

где х⁰ — постоянная составляющая (4.17), q и q' — коэф­фициенты гармонической линеаризации (4.18). Их вы­числение показано в примерах 4.6—4.10 раздела 4.2.

Подставим искомое решение (4.15) и (4.16) в результат

гар­монической линеаризации нелинейности (4.61) в задан­ное уравнение системы (4.59):

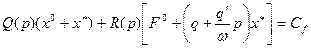
Выделим отсюда уравнение для постоянных составляю­щих:

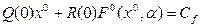(4.62)

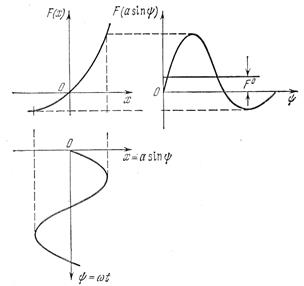
Рис.4.28. Возникновение несимметричных

колебаний

и уравнение для периодических составляющих:

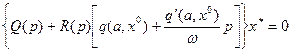(4.63)

Видно, что постоянная составляющая ( 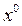) и колебатель­ная (α, ω) определяются не в отдельности, а только путем совместного решения этих уравнений.

Сначала из алгебраического уравнений (4.15) и (4.16) можно определить зависимость

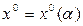(4.64)

Затем подставить эту зависимость в выражения 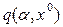и , и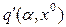меющиеся для заданной нелинейности. Тог­да получатся новые выражения и графики для q(α) и q'(α), включающие зависимость (4.64). В результате уравнение (4.63) приводится к виду (4.38). Методика решения задачи по определению α и ω остается прежней (раздел 4.3 или раздел 4.4), но с новыми выражениями и графи­ками для q(α) и q'(α).

Определение функции (4.64) упрощает­ся в двух случаях, а именно:

а) при несимметричной нелинейности и без внешнего воздействия вместо (4.62) имеем

;

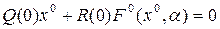б) при наличии нулевого полюса в передаточной
функции линейной части, когда 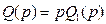, вместо (4.62) в общем случае получим

,

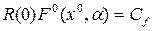а без внешнего воздействия, при несимметричной нели­нейности

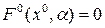
Например, при несимметричной нелинейности вида рис. 4.12, а в системе со свойством 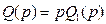, со­гласно примеру 4.10 раздела 4.2 получим

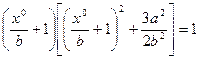
Этим определяется зависимость между величиной сме­щения 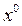и амплитудой α, после чего используется урав­нение (4.63).

Определение из уравнения (4.63) периодической со­ставляющей х*, т. е. величин α и ω, упрощается в случае однозначной нечетно-симметричной нелинейности 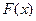. В этом случае, согласно (4.63), характеристическое урав­нение получает вид

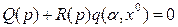(4.64)

а после подстановки 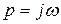аналогично (4.41) придем к уравнениям

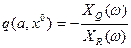
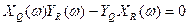
Сравнив эти уравнения с (4.41), получаем

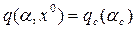, (4.65)

где 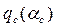относится к симметричным автоколебаниям в той же системе, определяемым согласно раздела 4.3. Сделав подстановку (4.64), будем иметь уравнение

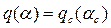, (4.66)

где 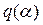—новое выражение или график, учитывающий зависимость (4.64).

Таким образом, при однозначной нелинейности часто­та ω несимметричных автоколебаний остается такой же, как и при симметричных, независимо от величины сме­щения 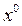. Амплитуда же несимметричных колебаний α, определяемая уравнением (4.65), зависит от смещения 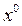и выражается через амплитуду симметричных автоко­лебаний α_с. Здесь не требуется решать уравнение (4.63).

Пример.4.14. В следящей системе (рис. 4.29) заданы 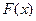в виде рис. 1.13 и передаточные функции:

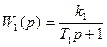
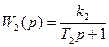
Рис.4.29. Следящая система с идеальной релейной

характеристикой

Гармоническая линеаризация нелинейности (раздел 4.2) при симметричных колебаниях дает

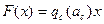
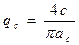
а при несимметричных —

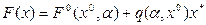(4.67)

где, согласно (4.32),

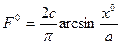
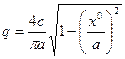(4.68)

Уравнение замкнутой системы относительно переменной х (рис. 4.29) имеет вид

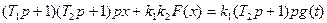(4.69)

При симметричных автоколебаниях ( 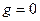) имеем характеристическое уравнение

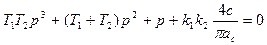
Подставив 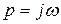, получим

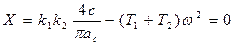
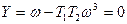
Откуда

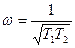
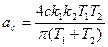(4.70)

Рассмотрим несимметричные автоколебания при зада­ющем воздействии 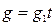. В соответствии с (4.62), (4.68) и (4.69) получаем уравнение для постоянных со­ставляющих

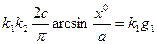
откуда находим

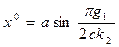(4.71)

Подстановка (4.71) в выражение для q (4.68) дает

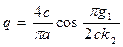
Теперь для определения амплитуды α несимметрич­ных автоколебаний используем уравнение (4.66), а имен­но

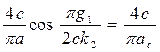
Откуда

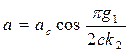, (4.72)

где α_с определяется соотношением (4.71). Тогда, соглас­но (4.71), постоянная составляющая (смещение) опре­деляется в виде

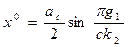(4.73)

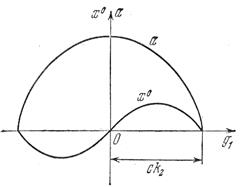
Рис.4.30. Зависимости

α и 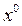от g₁

Частота же ω несимметричных автоколебаний будет прежней (формула 4.70).

Результаты (4.72) и (4.73) представлены графически на рис. 4.30.

Пример 4.15. Исследуем ту же систему (рис. 4.29), но с несимметричной нелинейностью 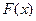вида рис. 4.31,а при задающем воздействии 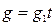. Уравнение системы:

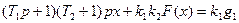
Причем 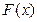вычисляется по формуле (4.67), где аналогично примеру 4.10 раздела 4.2 имеем

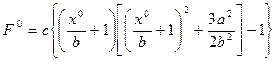(4.74)

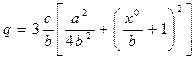(4.75)

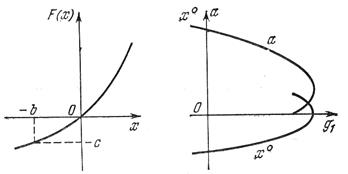
а) б)

Рис.4.31. Зависимости α и 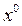от g₁ для

несимметричной нелинейности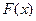

Уравнение для постоянных составляющих (4.62), с учетом того, что здесь 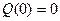, запишется в виде

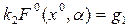
откуда согласно(4.74) имеем

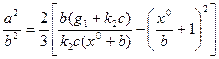(4.76)

Характеристическое уравнение для периодических со­ставляющих в соответствии с (4.62) запишется в виде

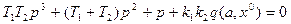
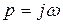После подстановки получаем

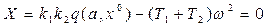
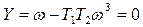
Откуда

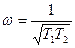
Последнее уравнение с подстановкой (4.75) и (4.76) приобретает вид

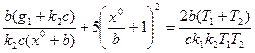
Отсюда определяется величина смещения 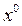, после чего вычисляется амплитуда α по формуле (4.76). Результа­ты представлены на рис. 4.31, б.

4.6. Контрольные вопросы к главе 4

1. Что составляет основу метода гармонической линеаризации?

2. Какой тип ряда используется для разложения сигнала нелинейного звена?

3. Каким свойством должна обладать линейная часть системы?

4. Что обуславливает неприменимость принципа суперпозиции в нелинейных системах?

5. Какими должны быть знаки параметров ξ и α для устойчивости периодического решения?

6. Что является критерием устойчивости периодического решения?

7. Каким способом определяется устойчивости периодического решения?

8. При каком типе корней характеристического уравнения получается периодическое решение?

9. Как определяется зависимость между величиной смещения и амплитудой?

10. Зависит ли частота несимметричных автоколебаний, при однозначной нелинейности, от величины смещения?