Вычисление коэффициентов гармонической линеаризации

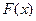Проиллюстрируем вычисление коэффициентов гармо­нической линеаризации на нескольких примерах: снача­ла для симметричных колебаний, а затем для несиммет­ричных. Предварительно заметим, что если нечетно-сим­метричная нелинейность однозначна, то, согласно (4.11) и (4.10), получаем

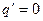
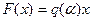(4.19)

причем при вычислении q (4.11) можно ограничиться интегрированием на четверти периода, учетверив резуль­тат, а именно

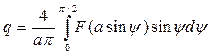(4.20)

Для петлевой нелинейности 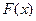(нечетно-симметрич­ной) будет иметь место полное выражение (4.10)

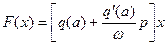(4.21)

причем можно пользоваться формулами

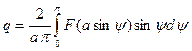
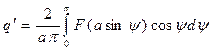(4.22)

т. е. удвоением результата интегрирования на полупериоде.

Пример 4.1. Найдем коэффициенты гармо­нической линеаризации для кубической нелинейности (рис. 4.4, a):

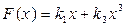
Воспользуемся формулами (4.22). В выражение для 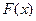вместо x подставим 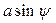и проинтегрируем (4.22). Получим:

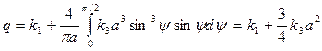
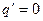
Зависимость 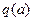показана на рис. 4.4,б. Из рис. 4.4,а видно, что при заданной амплитуде α прямая 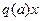уcредняет криволинейную зависимость 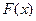на данном участке . Естественно, что крутизна 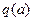на­клона этой усредняющей

Рис.4.4,а. Кубическая Рис.4.4,б. Зависимость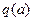

нелинейность

прямой 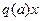увеличивается с увеличением амплитуды α (для кубической характе­ристики это увеличение происходит по квадратичному закону).

Пример 4.2. Исследуем петлевую релейную характе­ристику (рис. 4.5, а). На рис. 4.5,б представлена подын­тегральная функция 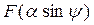для формул (4.22). Переключение реле имеет место при . Поэтому в момент переключения величина ψ₁ определяется выражением 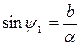. По формулам (4.22) получаем (для )

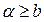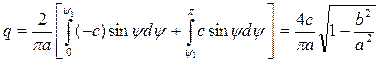
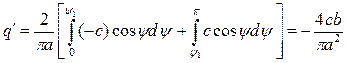(4.23)

а) б) в)

Рис. 4.5. Графики q(α) и q'(α)

На рис. 4.5, в изображены график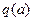и и . Первый из них показывает изменение крутизны наклона усредняющей прямой 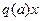с изменением α (рис. 4.5, а). Естественно, что 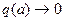при 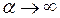, так как сигнал на выходе остается постоянным ( 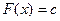) при любом неограниченном увеличении входного сигна­ла х. Из физических соображений ясно также, почему 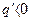. Это коэффициент при производной в формуле (4.21). Положительный знак давал бы опережение сиг­нала на выходе, в то время как гистерезисная петля дает запаздывание. Поэтому естественно, что 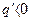. Абсолют­ное значение q' уменьшается с увеличением амплиту­ды α, так как ясно, что петля будет занимать тем мень­шую часть «рабочего участка» характеристики 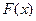, чем больше амплитуда колебаний переменной х.

Характеристика такой нелиней­ности (рис. 4.5, а), представляется в виде (4.13), причем амплитуда и фаза первой гармоники на выходе нелинейности имеют соответственно вид

,

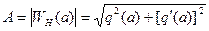
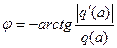где q и q' определены выше (рис. 4.5, в). Следовательно, гармоническая линеаризация переводит нелинейное ко­ординатное запаздывание (гистерезисную петлю) в экви­валентное запаздывание по фазе, характерное для ли­нейных систем, но с существенным отличием — зависимостью фазового сдвига от амплитуды входных колеба­ний, чего нет в линейных системах.

Пример 4.3. Возьмём однозначные релейные ха­рактеристики (рис. 1.13 и рис. 1.3). Аналогично предыдущему получаем соответственно

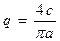
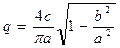(4.24)

q' = 0

что изображено на рис. 4.6, а, б, соответственно.

а) б)

Рис. 4.6. Зависимость 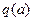для релейных ха­рактеристик

Пример 4.4. Исследуем характеристику с зоной не­чувствительности, линейным участком и насыщением (рис. 4.7, а). Здесь 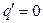, а коэффициент 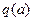имеет два варианта значений в соответствии с рис. 4.7, б, где для них построена :

1) при 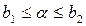, согласно (4.20), имеем

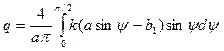
что с учетом соотношения 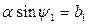дает

(4.25)

2) при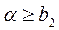

что с учетом соотношения 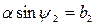дает

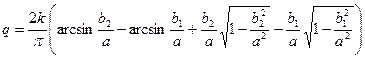(4.26)

Графически результат представлен на рис. 4.7, в.

а) в)

Рис.4.7. Графики для характеристики с зоной

не­чувствительности

Пример 4.5. Как частные случаи, соответствующие коэффициенты q(α) для характеристик (рис. 1.5 и 1.1) равны

при 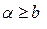(4.27)

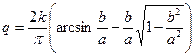при 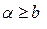(4.28)

что изображено графически на рис. 4.8, а, б. При этом для характеристики с насыщением (рис. 1.5) имеем 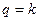при .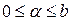

а) б)

Рис.4.8. Коэффициенты 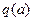для характеристик

на рис. 1.5 и рис. 1.1

Пример 4.6. Для случая кубической нелинейности 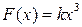по формуле (4.17) имеем

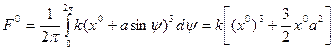(4.29)

а по формулам (4.18)

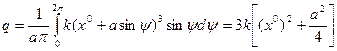
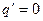(4.30)

Пример 4.7. Для петлевой релейной характеристики (рис. 1.10) по тем же формулам(4.17) и (4.18) имеем

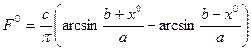(4.31)

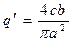(4.32)

Пример 4.8. Для характеристики с зоной нечувстви­тельности (рис. 4.9) будут иметь место те же выраже­ния F⁰ и q. Графики их представлены на рис. 4.9, а, б. При этом .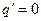

а) б)

Рис.4.9. Графики 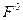и q для характеристики

с зоной нечувстви­тельности

Для идеальной же релейной характе­ристики (рис. 1.13) получаем

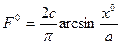
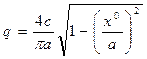(4.33)

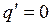
что изображено на рис. 4.10, а и б.

а) б)

Рис.4.10. Графики 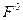и q для релейной

характеристики

Пример 4.9. Для характеристики с линейным участ­ком и насыщением (рис. 1.5) при имеем

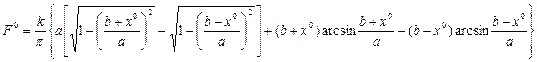(4.34)

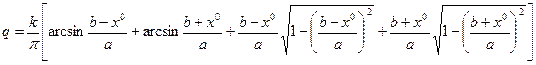(4.35)

В этом случае величина c на рис.1.5 равна .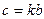

Эти зависимости представлены в виде графиков на рис. 4.11, а, б.

а) б)

Рис. 4.11. Графики для характеристики с линейным участ­ком и насыщением

Пример 4.10. Для несимметричной характеристики (рис.4.12,а)

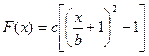
по формуле (4.17) находим

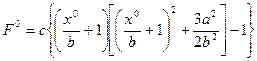
а по формулам (4.18)

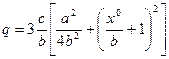
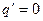
а) б) в)

Рис. 4.12. Зависимости , и q для несимметричной характеристики

Результаты изображены графически на рис. 4.12, б и в.

Полученные в этих примерах выражения и графики коэффициентов гармонической линеаризации будут ис­пользованы ниже при решении задач по исследованию автоколебаний, вынужденных колебаний и процессов управления.