Определение переходного процесса.

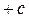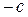Представим себе примерно возможный качественный вид процесса (рис. 3.1). Он разбивается на участки АВ, BD и т. д., внутри которых в соответствии с нелинейной характеристикой функция F(x) принимает постоянные значения или . Изобразим отдельно участки АВ и BD (рис. 3.2), отсчитывая время t на каждом из них от нуля.

Рис.3.1. Возможный

качественный вид

процесса

На участке АВ, согласно (3.1), уравнение системы

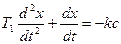
имеет первый интеграл в виде

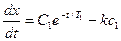(3.2)

а второй —

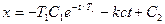(3.3)

Начальные условия: при 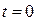, , 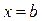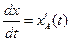. По ним из (3.2) и (3.3) находим

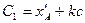(3.4)

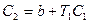(3.5)

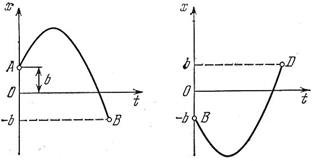
а) б)

Рис.3.2. Отдельное изображение

участков АВ и BD

На участке BD, согласно (3.1), имеем

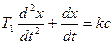
Первый интеграл этого уравнения

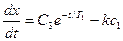(3.6)

а второй —

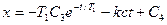(3.7)

Начальные условия для участка BD (в точке В) оп­ределяются на основании решения относительно точки В уравнения для предыдущего участка АВ. Из (3.2) находим

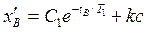(3.8)

где 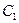известно из (3.4), а величина 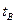определяется из уравнения (3.3) при условии 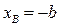, т. е.

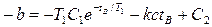
где 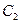известно из (3.4). Отсюда определяем 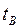и полу­ченное значение подставляем в формулу (3.8).

Таким образом, начальные условия для участка BD имеют вид

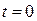
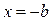
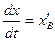
и, согласно (3.6), (3.7), получаем

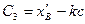
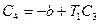
На следующем за точкой D участке снова, как и на АВ, будет решаться уравнение

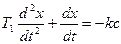
при этом произвольные постоянные определятся с учетом координат конца предыдущего участка BD и т. д.

3.1.2.Определение периодического решения (автоколеба­ний)

В этом случае расстояние AD по оси времени (рис. 3.1) является периодом автоколебаний. Вся кривая ABD после точки D должна повторяться в точности в том же виде. Вследствие нечетной симметрии характеристики (рис. 1.10) должна иметь место нечетная симметрия и полупериодов АВ и BD. Поэтому для определения перио­дического решения (автоколебаний) достаточно рассмот­реть один полупериод — участок АВ.

Обозначим через Т полупериод искомых автоколеба­ний. В силу периодичности решения начало и конец участка АВ должны удовлетворять равенствам

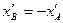(3.9)

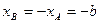(3.10)

при .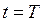

Формула(3.2) для конца отрезка принимает вид:

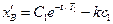
Используя (3.4) получим:

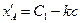
Полученные соотношения подставляем в (3.9):

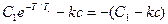
Откуда

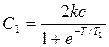(3.11)

Второе условие (3.10), согласно (3.3), запишется в виде

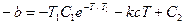
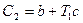
или

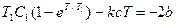
Подставив сюда выражение для 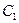из (3.11), придем к уравнению

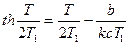(3.12)

с одной неизвестной величиной — полупериодом Т.

Трансцендентное уравнение (3.12) легко решается графически. Обозначим

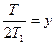
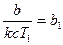
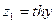
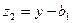
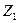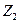Кривые и , согласно этим равенствам, изображены на рис. 3.3. Решением уравнения (3.10) будет точка ,

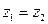т. е. точка пересечения кри­вых 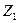и 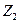(рис. 3.3). От­сюда находим полупериод Т автоколебаний. Частота ав­токолебаний

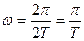
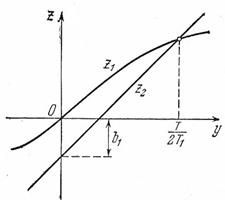
Рис.3.3. Графическое решение

трансцендентного уравнения

Амплитуда автоколебаний определится как 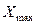на уча­стке АВ (рис. 3.1), т. е. из условия 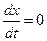. При этом из (3.2)

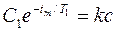(3.13)

где 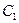определяется формулой (3.11), a 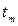— время t в точке максимума пока неизвестно. Из (3.13) с учетом (3.11) находим

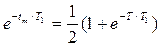
Откуда

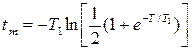
Далее по формуле (3.3) определим амплитуду автоко­лебаний:

,

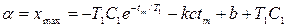где 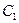известно из (3.11). В результате формула

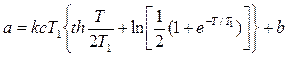
позволяет вычислить и амплитуду автоколебаний.