Исходные положения метода гармонической линеаризации

В предыдущих главах исследовались переходные про­цессы и автоколебания в нелинейных системах второго порядка. Этот материал весьма важен для получения на­глядного представления о некоторых особенностях пове­дения нелинейных систем по сравнению с линейными. Однако большинство реальных систем автоматического управления и регулирования описывается уравнениями более высокого порядка. В связи с этим в данной и в следующих главах будут рассмотрены методы исследова­ния нелинейных систем выше второго порядка.

Наиболее распространенным на практике для этих целей является метод гармонической линеаризации (метод гармонического баланса). Основу этого приближенного метода составляют следующие положения.

Пусть имеется нелинейное звено с характеристикой

любого из видов,

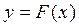(4.1)

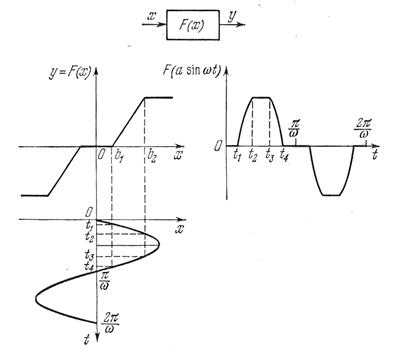
указанных в разделе 1.1 (например, на рис. 1.1 —1.11). Подадим на вход этого звена гармониче­ский сигнал 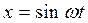. На выходе получим 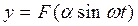. На рис. 4.1 дан пример графического представления функции 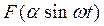(рис. 4.1, б) для за­данной нелинейной характеристики F(x) (рис. 4.1, а). Этот периодический выходной сигнал нелинейного звена можно разложить в ряд Фурье

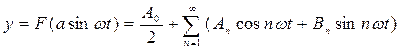(4.2)

где

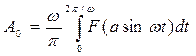(4.3)

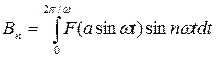(4.4)

Будем рассматривать нелинейную автоматическую систему с одной нели­нейностью 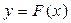. Тогда, выделив эту нелинейность в отдельное звено, можно всю остальную часть

а) б)

Рис. 4.1. Графическое представление

функции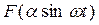

системы, какую бы сложную структуру она ни имела, объединить в единый блок — линейную часть (рис. 4.2). Передаточ­ную функцию линейной части обозначим

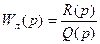(4.5)

и будем считать, что степень многочлена R(p) в числи­теле меньше, чем степень многочлена Q(p) в знаменателе. Тогда амплитудная частотная характеристика линейной части 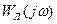(рис. 4.3) будет стремиться к нулю при 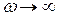. Начало этой частотной характеристики может иметь два варианта (1, 2, рис. 4.3) в зависимости от того, имеется или нет нулевой полюс в передаточной функции (4.5).

Допустим, что в данной замкнутой системе возможны собственные периодические колебания (автоколебания). Отметим на оси абсцисс (рис. 4.3) частоту первой гар­моники этих колебании ω и высшие гармоники 2ω, Зω, ...

Рис. 4.2. Нелинейная Рис. 4.3. АФЧХ

автоматическая линейной

система части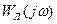

Предположим, что наша система обладает тем свойством, что величина амплитудной характеристики на частотах высших гармоник значительно меньше, чем для первой:

,

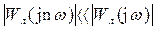Это свойство называется свойством фильтра нижних частот линейной части системы. При наличии свойства фильтра линейная часть системы (рис. 4.2) будет хорошо пропускать пер­вую гармонику нелинейных колебаний у и ослаблять все высшие гармоники. Поэтому переменная х на выходе не­линейного звена окажется близкой к синусоиде:

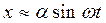(4.6)

Это обстоятельство усиливается еще тем фактом, что, как правило, амплитуды высших гармоник (4.4) переменной у хотя и не малы, но все же меньше, чем первой.

При несимметричных колебаниях появится еще посто­янная составляющая :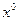

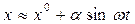(4.7)

Итак, базируясь на свойстве фильтра линейной части системы, будем считать, что собственные периодические колебания замкнутой нелинейной системы на входе нели­нейного звена х в первом приближении можно полагать синусоидальными (4.6) или (4.7). Выходную же вели­чину у нелинейного звена, содержащую в себе заметные высшие гармоники, надо определять при этом либо гра­фически, как на рис. 4.1, либо аналитически — по фор­муле (4.2). В итоге вся задача сводится к определению двух неизвестных: частоты ω и амплитуды α первой гармоники колебаний переменной х в случае симметрич­ных колебаний (4.6). В случае же несимметричных колебаний (4.7) речь будет идти о трех неизвестных: α, ω и постоянной составляющей .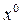

Для решения этой задачи необходимо исследовать только прохождение первой гармоники по всей замкнутой цепи, не учитывая пока высших гармоник переменной у, ибо в первом приближении считается, что они не прохо­дят на выход х линейной части системы.

Запишем выра­жение первой гармоники переменной у согласно (4.2):

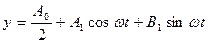(4.8)

отбросив высшие гармоники не потому, что они малы, а потому что они не нужны для определения первого приближения х.

Симметричные колебания. При этом в (4.8) 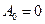. Обозначим

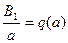
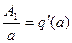(4.9)

Тогда (4.8) запишется в виде

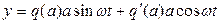
Но, заметив, что

,

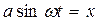
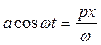где .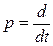

Получим

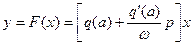(4.10)

Обозначим 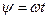, и согласно (4.4) и (4.9), имеем

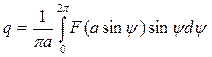
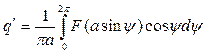(4.11)

Представление (4.10) называется гармонической ли­неаризацией нелинейности, а величины q и q' — коэффициентами гармонической линеаризации.

Правая часть выражения (4.10) линейна при 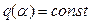, т. е. только для данного конкретного периоди­ческого решения. Но в целом она сохраняет нелинейные свойства, так как коэффициенты данного периодического решения зависят от искомого решения (от величины амп­литуды колебаний переменной х). Эта особенность гармо­нической линеаризации и позволит нам в дальнейшем исследовать с ее помощью основные свойства и процессы в нелинейных автоматических системах.

Гармонически линеаризованная передаточная функция нелинейного звена имеет вид

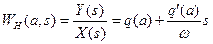(4.12)

Передаточная функция нелинейного зве­на в результате подстановки 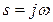выражается в форме

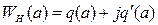(4.13)

Следовательно, передаточная функция нелинейности 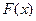зависит только от амплитуды и не зависит от частоты, в противоположность характеристикам линейных звеньев.

Несимметричные колебания. При этом, согласно (4.7), будем иметь

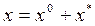(4.14)

где 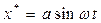. (4.15)

Поэтому в результате гармонической линеаризации вме­сто (4.10) —(4.11), согласно (4.8), (4.3) и (4.4), получим

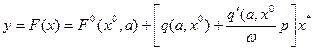(4.16)

где

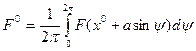(4.17)

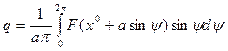
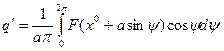(4.18)

Как видно из (4.16), выходная величина нелинейно­сти у содержит постоянную составляющую 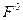и перио­дическую составляющую, выраженную как (4.15). 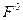зависит не только от 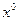и не только от α, но от обеих сразу. Это является существенным отличием нелинейного звена от линейного и обусловливает неприменимость здесь принципа суперпозиции, который составлял важное свойство линейных систем.