Система с логическим управлением. Учет временного запаздывания
Рассмотрим автоматическую систему угловой стабилизации объекта в среде без сопротивления (стабилизация аппарата в космосе). Структурная схема системы изображена на рис. 2.9. Уравнение динамики объекта, т. е. уравнение вращения объекта вокруг своей оси, имеет вид
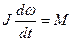 , (2.12)
, (2.12)
где J — момент инерции, ω — угловая скорость, М— вращающий момент со стороны системы управления. Будем считать, что вследствие некоторых внешних возмущений объект начал вращаться (например, в результате неидеальности процесса отделения от носителя при запуске), и рассмотрим его стабилизацию с помощью системы управления при отсутствии внешних возмущений.
Система управления (рис 2.9) состоит из двух измерителей: измерителя угла φ и измерителя угловой скорости ω, с которых сигналы u1и u2снимаются в релейной форме, показанной на рис. 2.10 Эти сигналы поступают в логическое устройство, вырабатывающее нелинейный закон управления в виде некоторой логической функции 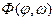 , которая служит управляющим воздействием на включение и выключение газовых сопел, создающих вращательный
, которая служит управляющим воздействием на включение и выключение газовых сопел, создающих вращательный

Рис.2.9. Система
управления
момент М.
Логическая управляющая функция 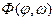 может быть сформирована в различных видах. В простейшем случае можно сформировать ее, как показано на рис. 2.11, использовав для переключений скачки сигналов u1и u2(рис. 2.10) при
может быть сформирована в различных видах. В простейшем случае можно сформировать ее, как показано на рис. 2.11, использовав для переключений скачки сигналов u1и u2(рис. 2.10) при 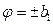 и
и 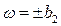 . При этом
. При этом 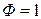 соответствует созданию управляющего момента в положительном направлении (против часовой стрелки),
соответствует созданию управляющего момента в положительном направлении (против часовой стрелки), 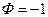 — в отрицательном направлении и
— в отрицательном направлении и 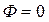 — отсутствию момента (все сопла выключены).
— отсутствию момента (все сопла выключены).
Указанный выбор логической функции Ф диктуется следующими соображениями. В нулевой зоне — 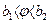 (рис. 2.10 и 2.11) нет сигнала от датчика угла. Устанавливаем
(рис. 2.10 и 2.11) нет сигнала от датчика угла. Устанавливаем 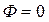 , так как объект находится вблизи требуемого положения
, так как объект находится вблизи требуемого положения 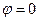 , и регулирующее воздействие не требуется. В I квадранте (рис. 2.11) имеем
, и регулирующее воздействие не требуется. В I квадранте (рис. 2.11) имеем 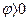 и
и 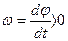 . Следовательно, угол φ увеличивается во времени — объект уходит от требуемого положения. Здесь устанавливаем
. Следовательно, угол φ увеличивается во времени — объект уходит от требуемого положения. Здесь устанавливаем 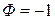 (направление вращающего момента противоположно направлению угловой скорости ω).
(направление вращающего момента противоположно направлению угловой скорости ω).
Аналогично в III квадранте, где знаки φ и ω отрицательные, включается 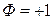 .
.
Что касается IV квадранта (рис. 2.11), то там 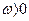 ,но
,но 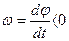 , т. е. объект сам возвращается к требуемому положению
, т. е. объект сам возвращается к требуемому положению 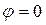 .
.

Рис.2.10. Скачки сигналов u1 и u2
при 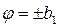 и
и 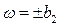
Здесь можно обойтись без управляющего момента. Устанавливаем 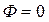 . Границей между областью
. Границей между областью 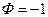 (в I квадранте) и областью
(в I квадранте) и областью 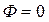 (в IV квадранте) назначаем величину
(в IV квадранте) назначаем величину 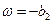 (рис. 2.11), когда сигнал с датчика угловой скорости имеет перескок с нуля к отрицательному значению (рис. 2.10). Аналогично поступаем и во II квадранте (рис. 2.11).
(рис. 2.11), когда сигнал с датчика угловой скорости имеет перескок с нуля к отрицательному значению (рис. 2.10). Аналогично поступаем и во II квадранте (рис. 2.11).
В соответствии с этой схемой строится логическое устройство (рис. 2.9). Его функционирование можно описать таблицей 2.1 выходного сигнала Ф в зависимости от входных.
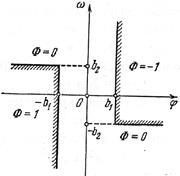
Рис.2.11. Выбор
логической функции Ф
Таблица 2.1. Зависимость
сигналов u1 от u2
| Сигнал u2 | Сигнал u1 | ||
| - | + | ||
| - | +1 | ||
| +1 | -1 | ||
| + | -1 |
Здесь приведен пример простейшей логики формирования закона управления. Можно выбирать и другие, более сложные,
в зависимости от требований, предъявляемых к системе по экономичности, точности, быстродействию и т. п.
Рассмотрим идеальную работу системы управления (без запаздывания сигналов по всей цепи звеньев). В этом случае уравнение системы управления запишется в виде
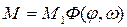 (2.13)
(2.13)
где 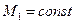 — величина управляющего момента, который создается включаемыми на постоянную тягу газовыми соплами;
— величина управляющего момента, который создается включаемыми на постоянную тягу газовыми соплами;
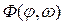 — логический закон управления, определяемый в данном случае приведенной выше таблицей или согласно графику на рис. 2.11.
— логический закон управления, определяемый в данном случае приведенной выше таблицей или согласно графику на рис. 2.11.
Общее уравнение системы, согласно (2.12) и (2.13), можно записать в виде

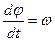
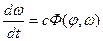 (2.14)
(2.14)
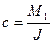
Физический смысл величины с — постоянное угловое ускорение вращения объекта под действием момента 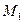 .
.
Дифференциальное уравнение фазовых траекторий:

 (2.15)
(2.15)
Фазовую плоскость ограничим по оси абсцисс значениями 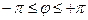 (рис. 2.12), причем для вращающегося тела точки
(рис. 2.12), причем для вращающегося тела точки 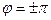 совпадают. Этим охватывается полный оборот объекта. Поскольку по оси абсцисс откладываются значения
совпадают. Этим охватывается полный оборот объекта. Поскольку по оси абсцисс откладываются значения 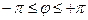 т. е. значения угла поворота тела вокруг оси, то мы фактически получаем цилиндрическую фазовую поверхность, которая здесь развернута на плоскость.
т. е. значения угла поворота тела вокруг оси, то мы фактически получаем цилиндрическую фазовую поверхность, которая здесь развернута на плоскость.
В области, где 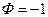 (рис. 2.12), уравнения (2.15) принимают вид
(рис. 2.12), уравнения (2.15) принимают вид
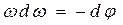
вследствие чего фазовые траектории являются параболами:
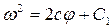 (2.16)
(2.16)
В области, где 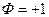 , имеем фазовые траектории
, имеем фазовые траектории
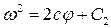 (2.17)
(2.17)
Наконец, в области, где  , получаем прямые линии
, получаем прямые линии
 (2.18)
(2.18)
Все указанные траектории приведены на рис. 2.12.
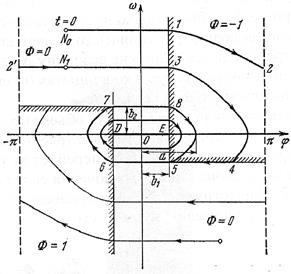
Рис.2.12. Фазовые траектории
Рассмотрим ход процесса. Пусть начальные условия определяются точкой N0 (рис. 2.12). Процесс пойдет согласно фазовой траектории N0 — 1—2. Точка 2 ( 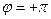 ) при вращении совпадает с точкой 2 (
) при вращении совпадает с точкой 2 (  ).
).
Поэтому дальше процесс пойдет в соответствии с фазовой траекторией 2—3—4—5. Как видно из рис. 2.12, точка N1 в которой угол φ равен начальному (в точке N0), означает, что объект совершил один полный оборот. Затем (траектория N1—3—4—5) он начал колебательное движение около своей оси. Начиная с точки 5, получаем замкнутую фазовую траекторию 5—6—7—8—5. Следовательно, объект входит в установившийся автоколебательный режим с амплитудой
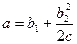 (2.19)
(2.19)
Своеобразие этого предельного цикла состоит, во-первых, в том, что снаружи фазовые траектории приближаются к нему не асимптотически, как было ранее в других задачах, а за конечное число колебаний (и за конечное время). В описанном выше процессе это было за один оборот плюс один размах колебания. Своеобразие этого предельного цикла заключается также в том, что фазовые траектории внутри него тоже замкнутые и окружают отрезок равновесия DE. Поэтому при малых начальных отклонениях, лежащих внутри предельного цикла, получаются периодические колебания, определяемые начальными условиями. В частности, состояние равновесия, возможное только при 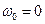 и
и 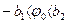 не является устойчивым. Особый отрезок DE имеет здесь свойства, аналогичные особой точке типа «центр» (рис. 1.39 и 1.40). Итак, установившимся режимом в данной системе являются автоколебания с амплитудой (2.19).
не является устойчивым. Особый отрезок DE имеет здесь свойства, аналогичные особой точке типа «центр» (рис. 1.39 и 1.40). Итак, установившимся режимом в данной системе являются автоколебания с амплитудой (2.19).
Введем теперь в рассмотрение временное запаздывание в системе управления. Пусть 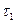 — величина запаздывания при включении газовых сопел, а
— величина запаздывания при включении газовых сопел, а 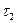 — при их выключении (
— при их выключении ( 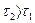 ). Поскольку к линии включения сопел
). Поскольку к линии включения сопел 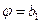 (рис. 2.12) объект подходит с постоянной скоростью (горизонтальные фазовые траектории), то за счет запаздывания включения сопел
(рис. 2.12) объект подходит с постоянной скоростью (горизонтальные фазовые траектории), то за счет запаздывания включения сопел 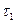 он перейдет за эту линию на величину
он перейдет за эту линию на величину 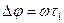 . Это значит, что линия включения займет теперь в координатах (φ, ω) наклонное положение (рис. 2.13). Аналогично и в III квадранте.
. Это значит, что линия включения займет теперь в координатах (φ, ω) наклонное положение (рис. 2.13). Аналогично и в III квадранте.
К линии же выключения сопел 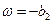 объект подходит с постоянным ускорением — с (параболическая фазовая траектория). Поэтому за счет запаздывания выключения сопел τ2 он перейдет за эту линию на величину
объект подходит с постоянным ускорением — с (параболическая фазовая траектория). Поэтому за счет запаздывания выключения сопел τ2 он перейдет за эту линию на величину 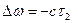 . Следовательно, линия выключения сопел
. Следовательно, линия выключения сопел 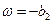 сместится вниз (рис. 2.13). Аналогично в левой полуплоскости линия выключения
сместится вниз (рис. 2.13). Аналогично в левой полуплоскости линия выключения 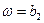 сместится вверх на величину
сместится вверх на величину 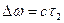 .
.
В соответствии с этим на рис. 2.13 нанесены фазовые траектории. Видно, что предельный цикл за счет запаздываний увеличился в размерах. Амплитуда его
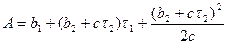 (2.20)
(2.20)
вместо прежней (2.19).

Рис. 2.13. Фазовые траектории с
запаздыванием
Изменится картина фазовых траекторий и внутри предельного цикла. Там включение сопел будет происходить на линиях FG и F1G1. Выключение же — на линиях FH и F1H1, которые получаются от перехода парабол за линии 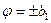 на
на 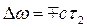 соответственно, причем отрезок Δ (рис. 2.13) определяется по формуле
соответственно, причем отрезок Δ (рис. 2.13) определяется по формуле
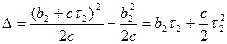
В результате внутри предельного цикла получаются расходящиеся спиралевидные фазовые траектории. Это соответствует расходящимся колебаниям системы, переходящим в предельный цикл. Здесь, как и в предыдущем случае, система попадает в автоколебательный режим извне не асимптотически, а за конечное число колебаний.
Рассмотренный подход к учету на фазовой плоскости временного запаздывания в системе эквивалентен в какой-то степени исследованию некоторых свойств системы выше второго порядка. Примерно таким же образом может влиять на поведение системы учет постоянных времени в системе управления.
Аналогичным способом можно производить учет временного запаздывания и в релейных системах автоматического управления.
2.4. Контрольные вопросы к главе 2
1. Затухает ли колебательный процесс до нуля?
2. Что такое «особый отрезок равновесных состояний?
3. Какую фазовую плоскость называют многолистной?
4. Какой процесс называется скользящим?
5. Какой вид имеют фазовые траектории в системе со скользящим процессом?
6. Является ли начало координат равновесным состоянием при скользящим процессе?
7. Зависит ли закон движения точки в скользящим процессе от параметров прямой цепи системы?
8. Чем определяется выбор логической функции в системе с логическим управлением?
9. В чем состоит особенность предельного цикла в системе с логическим управлением?
10. Изменяется ли картина фазовых траекторий внутри предельного цикла при учете запаздывания?
Дата добавления: 2020-10-25; просмотров: 708;











