Переходные процессы и автоколебания релейной системы
Рассмотрим систему с релейной характеристикой общего вида. Уравнение динамики объекта (рис. 2.1) имеет вид
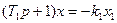 (2.1)
(2.1)
а уравнение регулятора
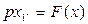 (2.2)
(2.2)
где F(х) — релейная характеристика (рис. 1.11). Общее уравнение динамики системы найдем, если продифференцируем уравнение (2.1)
| |
Рис. 2.1. Система с релейной
характеристикой общего вида
и затем подставим в него (2.2). В результате получим выражение
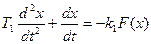 ,
,
которое можно представить в виде

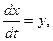
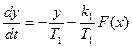 (2.3)
(2.3)
Отсюда получим дифференциальное уравнение фазовых траекторий
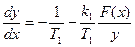 (2.4)
(2.4)
Как видно из заданной характеристики (рис. 2.1,б), нелинейную функцию F(х) можно описать следующим образом:
если 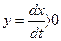 , то
, то

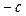 при
при 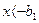
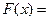 0 при
0 при 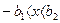
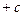 при
при 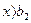
если 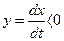 , то
, то

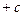 при
при 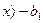
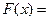 0 при
0 при 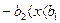
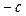 при
при 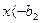
В связи с этим на фазовой плоскости (х, у) можно выделить три области: 1) 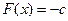 ; 2)
; 2) 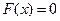 ; 3)
; 3) 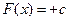 . Эти три области разделены прямыми (на рис. 2.2 они показаны штриховыми линиями), которые называются линиями переключения.
. Эти три области разделены прямыми (на рис. 2.2 они показаны штриховыми линиями), которые называются линиями переключения.
Такую фазовую плоскость называют многолистной. На каждом листе (1, 2, 3) получится свой вид фазовых траекторий. По линиям переключения эти листы «сшиваются». Фазовые траектории непрерывно переходят с одного листа на другой (за исключением некоторых особых случаев, где они встречаются).
В области 1 ( 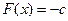 ) уравнение (2.4) принимает вид
) уравнение (2.4) принимает вид
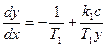
Проинтегрировав его, получим уравнение фазовых траекторий в области 1:
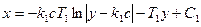 (2.5)
(2.5)
Фазовые траектории заканчиваются фазовой траекторией, уравнение которой: 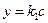 . Такие фазовые траектории изображены в области 1 на рис. 2.2. Направление их определяется в соответствии с рассмотренным выше правилом (рис. 1.9).
. Такие фазовые траектории изображены в области 1 на рис. 2.2. Направление их определяется в соответствии с рассмотренным выше правилом (рис. 1.9).
В области 2 ( 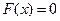 )уравнение (2.4) примет вид
)уравнение (2.4) примет вид
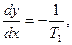
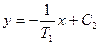
Фазовые траектории — прямолинейные отрезки (см. область 2на рис. 2.2).
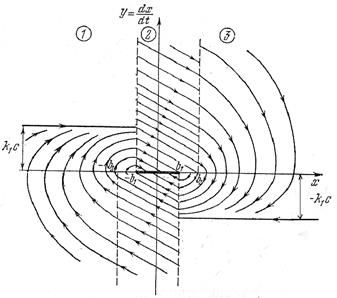
Рис.2.2. Фазовые траектории
Наконец, в области 3 ( 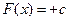 )уравнение (2.4) примет вид
)уравнение (2.4) примет вид
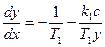
откуда, аналогично (2.5), уравнение фазовых траекторий будет
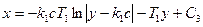 (2.6)
(2.6)
Фазовые траектории в области 3 заканчиваются фазовой траекториейуравнение которой: 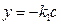 .
.
В целом фазовые траектории принимают спиралевидную форму. Это соответствует затухающим колебательным процессам. Однако колебательный процесс затухает не до нуля, а до некоторого произвольного значения (рис. 2.2, 2.3)
в интервале 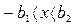 ,
, 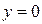 , т. е. внутри зоны нечувствительности реле (рис. 1.11). Таким образом, вместо особой точки здесь получается особый отрезок равновесных состояний,показанный утолщенной линией на рис. 2.2.
, т. е. внутри зоны нечувствительности реле (рис. 1.11). Таким образом, вместо особой точки здесь получается особый отрезок равновесных состояний,показанный утолщенной линией на рис. 2.2.
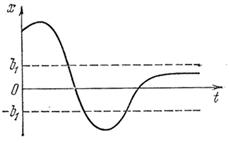
Рис.2.3. Затухающий
колебательный процесс
По какой из фазовых траекторий пойдет переходный процесс в системе, определяется начальными условиями 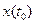 ,
, 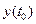 .
.
Рассмотрим теперь частные случаи.
В случае релейной характеристики с зоной нечувствительности без петель (рис. 1.3)картина фазовых траекторий будет аналогична изображенной на рис. 2.2, с той разницей, что теперь ,т. е. линии переключения будут прямыми без излома на оси х: 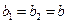 .
.
В случае чисто петлевой гистерезисной релейной характеристики(рис. 1.10)будет отсутствовать область 2(рис. 2.2). В этом случае имеем

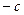 при
при 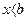
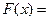
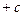 при
при 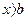
когда

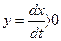
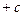 при
при 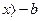
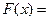
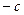 при
при 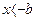
когда
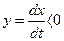
Этим определяются линии переключения (штриховые линии на рис. 2.4). Слева от них строим фазовые траектории по уравнению (2.5), а справа — по уравнению (2.6). Это и показано на рис. 2.4. Поскольку ясно видно, что снаружи фазовые траектории образуют сходящиеся спирали, а изнутри расходящиеся, то где-то среди них должен быть предельный цикл, к которому они все сходятся. Он выделен утолщенной замкнутой линией (рис. 2.4). Это устойчивый предельный цикл, отвечающий автоколебаниям. Амплитуда их определяется точкой пересечения предельного цикла с осью х. Физически такое решение оправдано, ибо в соответствии с нелинейной характеристикой (рис. 1.10) реле не имеет равновесного состояния. Автоколебания происходят около петли реле с амплитудой, несколько превышающей половину ширины петли b.
Установившийся режим работы такой системы автоматического регулирования является автоколебательным. Так работают, например, вибрационные регуляторы напряжения сети постоянного тока.
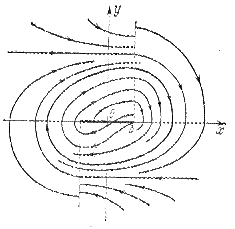
Рис.2.4. Устойчивый предельный цикл
Параметры системы должны быть выбраны так, чтобы амплитуда и частота автоколебаний находились в допустимых пределах.
Дата добавления: 2020-10-25; просмотров: 726;











