Система со скользящим процессом

Проиллюстрируем понятие скользящего процесса на простом примере. Пусть задана система автоматического регулирования (рис. 2.5), уравнения динамики которой имеют вид

Рис.2.5. Система автоматического

регулирования

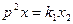
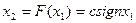
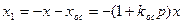
где 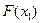- релейная характеристика вида (рис. 1.13).

Эти уравнения можно представить в виде

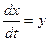
(2.7)

Дифференциальное уравнение фазовых траекторий:

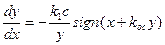(2.8)

Линия переключения на фазовой плоскости (х, у), описывается уравнением

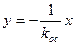(2.9)

Она показана на рис. 2.6. Справа от этой линии 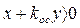. Поэтому уравнение фазовых траекторий (2.8) примет вид

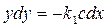
откуда

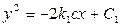
Таким образом, фазовые траектории — это параболы, ветви которых направлены в отрицательную сторону оси х. Положение вершины параболы определяется произ­вольной постоянной С₁, т. е. начальными условиями пере­ходного процесса 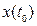, 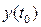. Эти параболы изображены на рис. 2.6 справа от линии переключения Направление, движения изображающей точки М по параболам опреде­ляется прежним правилом (рис. 1.9).

Слева от линии переключения 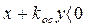, а урав­нение фазовых траекторий (2.8) имеет вид

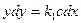
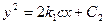
Эти параболы также изображены на рис. 2.6 слева от линии переключения. Видно, что на отрезке линии пере­ключения АВ

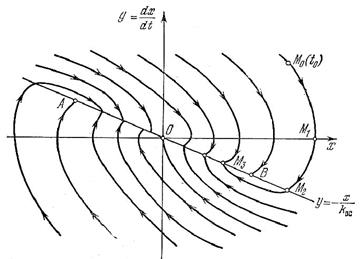
Рис.2.6. Линия переключения

на фазовой плоскости

фазовые траектории встречаются, упираясь в этот отрезок. Это можно расшифровать следующим об­разом. Пусть процесс идет по фазовой траектории 1 (рис. 2.7), Как только фазовая траектория пересечет линию переключения ОА, вступит в свои права фазовая траектория 2, которая вернет процесс к отрезку ОА. Но тут встретится фазовая траектория 3 и т. д. В результа­те изображающая точка путем вибраций около линии переключения переместится к началу координат 0.

Такой ход процесса соответствует переклю­чениям релейного эле­мента (рис. 1.13) с большой частотой.

Рис.2.7. Вибра­ции

Тео­ретически частота пере­ключения бесконечна, а амплитуда вибра­ций, изображенных на рис. 2.7, стремится к нулю. Следовательно, теоретически изобра­жающая точка скользит по линии переключения к началу координат — к равновесному состоянию. Процесс такого рода называется скользящим про­цессом.

Найдем закон движения в скользящем процессе. На линии переключения, согласно (2.9), если учесть первое из уравнений (2.7), имеет место уравнение

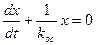(2.10)

Решением этого уравнения является

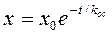
где значения 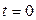и считаются в момент попа­дания изображающей точки на линию скользящего про­цесса.

Здесь важно отметить следующее. Нелинейная система второго порядка (2.7) на участке скользящего процесса вырождается в линейную систему первого порядка (2.10). При этом закон движения в скользящем процессе не за­висит от параметров прямой цепи системы и определяет­ся только коэффициентом обратной связи. Например, при начальном положении 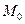(рис. 2.6) получим фазовую траекторию , переходящую в скольжение по линии AB. Такой фазовой траектории соответствует про­цесс во времени x(t), изображенный на рис. 2.8, где, как и ранее, отмечены характерные точки.

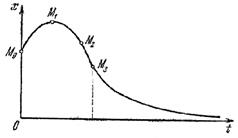
Рис.2.8. Про­цесс

во времени x(t)

Найдем положение концов отрезка скользящего про­цесса А и В на фазовой плоскости (рис. 2.6). Очевидно, что в этих точках касательные к параболам совпадают с линией переключения. Это условие, согласно (2.9), мож­но записать в виде

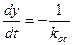(2.11)

тогда из уравнения фазовых траекторий (2.8) получим для точек А и В соответственно условие (2.11) в виде

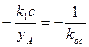, следовательно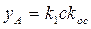

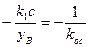, следовательно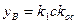

Следовательно, отрезок скользящего процесса АB тем больше, чем больше коэффициенты усиления прямой цепи и обратной связи.