Основные положения классической термодинамики. Энтропия. Принцип возрастания энтропии

Остановимся на некоторых положениях и результатах термодинамики, имеющих концептуальное, основополагающее значение для всего естествознания.

Важной характеристикой термодинамической системы является ее внутренняя энергия U - сумма энергий хаотического (теплового) движения частиц системы и энергий их взаимодействия друг с другом. Внутренняя энергия является функцией состояния системы, то есть зависит только от текущего состояния, но не зависит от способа, которым было получено это состояние. Бесконечное малое приращение внутренней энергии системы является поэтому полным дифференциалом и обозначается dU (см. подраздел 6.3.).

Внутренняя энергия системы может быть изменена двумя способами: посредством совершения работы либо передачи теплоты от внешних тел системе или наоборот. Отличие этих двух способов передачи энергии следующее. Передача энергии путем совершения работы сопровождается или перемещением внешних тел, с которыми взаимодействует система, или изменением полей, воздействующих на систему, то есть совершение работы обязательно сопровождается макроскопическими процессами. Типичный пример: газ в цилиндре, расширяясь и перемещая поршень, совершает работу против внешних сил.

Напротив, передача теплоты не сопровождается макроскопическими изменениями. При этом энергия передается на «микроскопическом уровне» от тела с большей энергией движения частиц телу, частицы которого имеют меньшую энергию движения. Передача теплоты осуществляется посредством теплопроводности, теплового излучения и конвекции (перемешивания жидкости или газа).

Количество теплоты, также как и работа, не является функцией состояния, и ее бесконечно малое количество обозначается .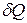

Одной из основ термодинамики является первое начало термодинамики, выражающее всеобщий закон сохранения энергии применительно к тепловым процессам. Оно гласит: количество теплоты Q, сообщаемое системе, расходуется на изменение его внутренней энергии 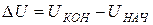и совершение работы A системой против внешних сил:

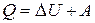. (7.12)

Для элементарного (бесконечно малого) процесса первое начало термодинамики имеет вид:

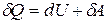. (7.13)

Если система не получает, а отдает теплоту, то величины Q и 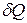в формулах (7.12) и (7.13) отрицательны, так же, как и A и 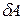в случае, если внешние силы совершают работу над системой.

Если совершение работы вызвано равновесным изменением объема системы, то при элементарном изменении объема dV давление в системе можно считать постоянным и применить формулу работы при изобарном процессе, известную из школьного курса физики:

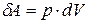. (7.14)

Отметим, что совершение работы не обязательно связано с изменением объема. Например, капля жидкости, изменяя форму и площадь своей поверхности, совершает работу по растяжению ограничивающей каплю внешней поверхности, находящейся в натянутом состоянии. Объем капли остается при этом неизменным. В ферромагнитном материале при изменении внешнего магнитного поля совершается работа по намагничиванию или размагничиванию материала; при этом изменение объема пренебрежимо мало.

Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии за один период 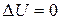. Тогда, согласно первому началу термодинамики, 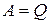, то есть вечный двигатель первого рода - периодически работающий двигатель, который совершал бы большую работу, чем сообщаемая ему извне энергия - невозможен (это утверждение есть одна из формулировок первого начала термодинамики).

Первое начало, запрещая тепловые процессы, в которых нарушается закон сохранения энергии, в частности запрещая существование вечного двигателя первого рода, тем не менее, разрешает протекание многих тепловых процессов, невозможных в действительности. Так, первое начало термодинамики разрешает, чтобы при контакте холодного и нагретого тел теплота переходила от холодного тела к более нагретому; первое начало требует лишь, чтобы количество теплоты, взятое у холодного тела, равнялось количеству теплоты, переданному более теплому телу. Первое начало термодинамики также не запрещает существование вечного двигателя второго рода - периодически работающего двигателя, который все полученное извне тепло превращает в полезную работу, то есть имеет коэффициент полезного действия, равный 100 %.

Таким образом, первое начало термодинамики не в полной мере описывает закономерности тепловых процессов - оно не указывает направление их протекания. Поэтому для адекватного описания реальности первое начало дополняют вторым началом термодинамики.

Приведем первые, так называемые качественные формулировки второго начала, которое должно было указать направление протекания тепловых процессов:

1. Невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к более нагретому (Р. Клаузиус, 1850 г.).

2. Невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения одного тела, то есть невозможен вечный двигатель второго рода (У. Томсон, 1851 г.).

Чтобы придать второму началу термодинамики количественную форму, Р. Клаузиус ввел понятие энтропии (1865 г.). Это понятие стало одним из важнейших для термодинамики и статистической физики. Из физики понятие энтропии широко распространилось по всему естествознанию, проникло в информатику, современные математические экономические и социологические теории.

Пусть 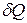- элементарное количество теплоты, сообщаемое телу нагревателем с абсолютной температурой T. Если процесс теплопередачи обратим, то температура тела бесконечно мало отличается от температуры нагревателя, то есть также равна T. Энтропией S тела называется величина, элементарное приращение которой dS при обратимом процессе таково

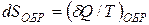. (7.15)

В отличие от количества теплоты, энтропия S есть функция состояния системы и ее бесконечно малое приращение должно обозначаться dS.

Если процесс необратим, то равенство (7.15) превращается в неравенство:

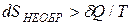. (7.16)

Замену равенства на неравенство можно пояснить на примере необратимого нагревания тела, при котором его температура 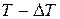отличается от температуры нагревателя T на конечную величину 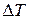. Как следует из формулы (7.15), приращение энтропии тела в этом случае равно

.

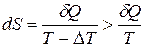Формулы (7.15) и (7.16) можно объединить в одну:

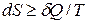, (7.17)

в которой знак равенства относится к обратимым, знак неравенства – к необратимым процессам.

Для изолированной системы 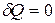и (7.17) сводится к соотношению

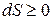. (7.18)

Это соотношение и есть математическая запись количественной формулировки второго начала термодинамики: энтропия изолированной системы не убывает. Иначе говоря, энтропия изолированной системы может либо возрастать при необратимых процессах ( 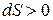), либо, достигнув максимального значения в равновесном состоянии системы, оставаться неизменной (dS=0). Также и при обратимых процессах в изолированной системе dS=0.

Поскольку все реальные процессы в изолированных системах необратимы, то все они ведут к увеличению энтропии (принцип возрастания энтропии).

Все качественные формулировки второго начала и формулировка на основе соотношения (7.18) эквивалентны, то есть следуют одна из другой.

Приведенное определение энтропии не вполне объясняет смысл этой величины. Наиболее наглядное истолкование понятия энтропии дает статистический метод. Познакомимся со статистическим смыслом энтропии.

Состояние макроскопического тела, образованного огромным количеством частиц, может быть задано с помощью макроскопических, характеризующих тело в целом, термодинамических параметров, таких как объем, давление, температура, внутренняя энергия и др. Охарактеризованное такими параметрами состояние называется макросостоянием.

Состояние макроскопического тела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело частиц, то есть их координаты и импульсы, называется микросостоянием.

Всякое макросостояние тела может быть осуществлено одним или несколькими различными способами, каждому из которых соответствует некоторое микросостояние тела. Например, макросостояние воздуха, заполняющего комнату, может быть осуществлено множеством способов, так как, например, меняя местами две частицы, мы получаем новое микросостояние при неизменном макросостоянии.

Термодинамической вероятностью или статистическим весом 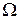некоторого макросостояния тела называется число разных микросостояний, соответствующих данному макросостоянию.

Чтобы пояснить понятие термодинамической вероятности, рассмотрим способы распределения частиц газа по сосуду, мысленно разделенному на две половины. Макросостояние будет характеризовать число частиц, находящихся в каждой половине сосуда. Состояние каждой частицы будет характеризовать то, в какой половине сосуда она находится; скорости частиц принимать во внимание не будем. Конечно, такое описание состояния частиц не является полным, но оно достаточно для того, чтобы выяснить статистические закономерности поведения систем из большого числа частиц.

Пусть в сосуде находятся четыре частицы. Считаем, что они пронумерованы и по номерам мы можем отличить их друг от друга, а также, что вероятности нахождения каждой из них в любой половине сосуда одинаковы (см. рисунок 7.3).

Рисунок 7.3. К определению понятия термодинамической вероятности.

В таблице 7.1 приведены все макросостояния системы (число частиц в каждой половине), микросостояния (распределение частиц по половинам), реализующие эти макросостояния, термодинамические вероятности 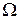макросостояний и их обычные вероятности P, равные статистическому весу 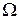макросостояния, отнесенному к общему числу всех возможных микросостояний.

Таблица 7.1 – Макро- и микросостояния системы из четырех частиц.

Макросостояния	Микросостояния	Термодинамическая вероятность	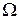Обычная Вероятность
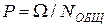
Число частиц слева	Число частиц справа	Номера частиц слева	Номера частиц слева
		-	1, 2, 3, 4		1/16
			2, 3, 4 1, 3, 4 1, 2, 4 1, 2, 3		4/16=1/4
		1, 2 1, 3 1, 4 2, 3 2, 4 3, 4	3, 4 2, 4 2, 3 1, 4 1, 3 1, 2		6/16=3/8
		1, 2, 3 1, 2, 4 1, 3, 4 2, 3, 4			4/16=1/4
		1, 2, 3, 4	-		1/16
Всего микросостояний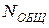

Из приведенных данных следует, что наиболее вероятно состояние, когда в обеих половинах сосуда находится одинаковое число частиц. Вероятность того, что все частицы скопятся в одной половине сосуда (левой или правой) меньше, но в данном случае еще достаточно велика: 1/16+1/16=2/16=1/8.

Нетрудно убедиться, что с увеличением общего числа частиц вероятность их равного разделения по половинам сосуда будет оставаться максимальной, несколько меньшей будет вероятность состояний с небольшим различием числа частиц слева и справа, а вероятность состояний со значительным различием числа частиц в разных половинах станет ничтожно малой. В подтверждение этому в таблице 7.2 перечислены некоторые макросостояния аналогичной системы из 24 частиц, их термодинамические и обычные вероятности.

По определению равновесным является такое макросостояние системы, в котором она не имеет тенденции к изменению с течением времени. Ясно, что наименее выражена такая тенденция у состояния с наибольшей вероятностью, то есть с наибольшим статистическим весом. Поэтому равновесное состояние есть состояние, вероятность которого максимальна.

Таблица 7.2 - Макро- и микросостояния системы из 24 частиц.

Макросостояния	Термодинамическая вероятность	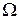Обычная вероятность P
Число частиц слева	Число частиц справа
… …	… …	… 1 307 504 1 961 256 2 496 144 2 704 156 2 496 144 1 961 256 …	6·10-8 1.4·10-6 1.6·10-5 … 7.8·10-2 0.117 0.149 0.161 0.149 0.117 … 1.46·10-6 6·10-8
Всего 224=16 777 216 микросостояний

Поскольку вероятность состояний, близких к равновесным, тоже достаточно велика, то и в этих состояниях система будет пребывать некоторое время. Этим объясняется неизбежность флуктуаций параметров, то есть их отклонений от средних равновесных значений, даже у равновесной системы. Но эти отклонения кратковременны и незначительны, так как вероятность состояний, сильно отличающихся от равновесных, весьма мала.

Статистическая физика вскрывает природу необратимости реальных процессов. Предположим, что вначале все частицы газа находились в одной половине сосуда, отделенной перегородкой от другой пустой половины. Если перегородку убрать, газ самопроизвольно распространится на весь сосуд. Этот процесс необратим, так как вероятность того, что частицы самопроизвольно, без воздействия извне, вновь соберутся в одной половине, фактически равна нулю.

Как показывает сравнение примеров, приведенных в таблицах 7.1 и 7.2 для 4 и 24 частиц, с увеличением числа частиц вероятности значительных отклонений от равновесного состояния (когда, например, одна из половин сосуда пуста) уменьшаются. Для реальных тел, содержащих огромное число частиц, вероятности значительных отклонений малы настолько, что за все время существования тела они не имеют шансов осуществиться, то есть фактически никогда не осуществляются.

Л. Больцмана в работах 1872-77 гг. доказал, что энтропия S системы в каком-либо ее макросостоянии пропорциональна натуральному логарифму термодинамической вероятности данного состояния:

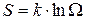, (7.19)

где k=1.38·10^-23 Дж/К - постоянная Больцмана.

Из сказанного вытекают следующие свойства энтропии.

1. Энтропия есть мера вероятности макросостояния, в котором находится тело (система). Увеличение 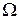в соответствии с (7.19) ведет к увеличению S.

1. Энтропия изолированной системы при протекании в ней необратимых процессов возрастает, ибо изолированная система самопроизвольно переходит из менее вероятного в более вероятные состояния.

2. Энтропия системы, находящейся в равновесном состоянии, максимальна.

Отметим еще раз, что из-за неизбежности флуктуаций эти утверждения, как и многие другие термодинамические закономерности, не имеют абсолютно строгого характера. Вернее сказать, термодинамические закономерности строго выполняются для величин, усредненных по большому числу частиц или по большому промежутку времени, но допускают локальные кратковременные отклонения.

В приведенных выше примерах распределения частиц газа по сосуду мы при описании микросостояний игнорировали наличие у частиц скоростей. Можно показать, что для идеального газа вне силовых полей в условиях изоляции равновесным является состояние с равномерным распределением частиц газа по предоставленному объему, одинаковой по всему объему температурой и максвелловским распределением частиц газа по скоростям. При наличии внешних силовых полей равновесным является состояние с одинаковой во всем объеме температурой, максвелловским распределением частиц по скоростям и больцмановским распределением по энергиям.

Статистическое истолкование смысла энтропии связано также с понятиями порядка и беспорядка (хаоса).

Состояние системы, осуществляемое одним или малым числом способов, называется упорядоченным. Вероятность этого состояния мала, и, следовательно, энтропия системы в таком состоянии также мала. Состояние, осуществляемое многими различными способами, называется беспорядочным или хаотическим или случайным. Его вероятность и соответствующая энтропия велики. Таким образом, энтропия системы есть количественная мера степени беспорядка в системе. Следовательно, второе начало термодинамики означает, что степень беспорядка в изолированной системе не убывает, она может либо возрастать, либо оставаться постоянной, достигнув максимального значения.

Переход из упорядоченного состояния в неупорядоченное, сопровождающийся ростом энтропии, проиллюстрируем на примере нагревания кристалла. Идеальная кристаллическая решетка при абсолютном нуле представляет собой идеально упорядоченную систему, так как может быть реализована единственным способом: строгим размещением всех частиц в узлах кристаллической решетки (если не учитывать возможность перестановки частиц). Состояния кристалла при 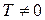, когда частицы могут совершать колебания у положений равновесия, могут быть реализованы множеством различных способов, а после разрушения решетки и перехода вещества в жидкое или газообразное состояние - еще большим числом способов. То есть при переходе от кристалла при абсолютном нуле к нагретому газу беспорядок в системе возрастает.

Обобщением примера с нагреванием кристалла является тепловая теорема Э. Нернста (1906 г.), называемая иногда третьим началом термодинамики: энтропия всякого тела стремится к нулю при стремлении к нулю абсолютной температуры:

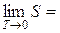0. (7.20)

Неочевидным, но логичным следствием приведенной формулировки тепловой теоремы Нернста является другая формулировка: путем конечной последовательности термодинамических процессов нельзя достичь абсолютного нуля.

Понятия порядка и беспорядка (хаоса) из чисто физических с течением времени стали общенаучными. Приведем примеры упорядоченных и неупорядоченных систем из различных областей.

Уже приведенный пример из физики: газ заполняет лишь часть сосуда. Вероятность и энтропия такого состояния малы – это упорядоченное состояние. Газ, распространившийся по всему сосуду – менее упорядоченная система.

В технике: упорядоченная система – механизм, в котором каждая деталь находится на своем, единственно возможном месте. Неупорядоченная система – перемешанные или, более того, расплавленные детали этого механизма.

В информатике: текст, сложенный из карточек с символами (буквами, знаками препинания и т.п.). Карточки расположены в единственно возможном порядке. Их перестановка искажает смысл текста. Это – упорядоченная система. Противоположность – перемешанные карточки с символами.

В биологии: живой организм, в котором органы, клетки и даже молекулы расположены упорядоченно, в нужной последовательности. Противоположность – продукты распада этого организма.

В социологии: упорядоченная система - хорошо организованная общность людей (производственный коллектив, спортивная команда, общественная организация), в которой каждый член занимает свое, соответствующее его возможностям место. Противоположность – дезорганизованная толпа.

Обратим внимание, что упорядоченные системы функционально ориентированны, то есть способны выполнять определенную функцию. Сжатый газ, расширяясь, совершает работу. Механизм выполняет определенные операции. Текст – передает информацию. Живой организм – растет, развивается, размножается. Организованный коллектив – выполняет социальные функции.

Общенаучное значение второго начала термодинамики заключается в том, что оно утверждает, что все естественные процессы, протекающие в замкнутых системах, ведут к росту энтропии, то есть увеличению хаотичности, дезорганизации этих систем, утрате функциональности, деградации.

Еще одним концептуальным аспектом второго начала термодинамики является установление неравноценности различных форм движения. Для физической формы движения это особенно ясно следует из качественной формулировки Томсона. Механическую энергию движения и взаимодействия макроскопических тел можно полностью превратить в энергию хаотического (теплового) движения частиц тел, например, благодаря трению. Обратное – полное превращение полученного телом тепла в механическую энергию путем совершения работы - оказывается невозможным. В более общем смысле, энергия упорядоченного движения и взаимодействия макроскопических объектов (кинетическая и потенциальная энергия макроскопических тел, энергия электрического тока, энергия электромагнитного поля, энергия химических соединений) при необратимых процессах (а все реальные процессы фактически необратимы) может полностью переходить в энергию хаотического теплового движения частиц. Обратное же полное преобразование энергии хаотического движения в энергию упорядоченного движения и взаимодействия невозможно.

Иначе, второе начало термодинамики, не отрицая количественной неуничтожимости движения, утверждает неизбежность его качественной деградации - перехода от организованных, упорядоченных форм к хаотическому тепловому движению. Кроме того, принципу возрастания энтропии соответствует стремление к равномерному распределению частиц и температуры в пространстве. Поэтому этот принцип означает, что все процессы в изолированных системах в конечном итоге ведут к выравниванию температуры и разрушению сформированных объектов и структур, то есть к переходу структурированной материи в однородное бесформенное состояние с постоянной по объему температурой, в котором нет упорядоченных движений, а вся энергия есть энергия хаотического теплового движения частиц.

Можно представить себе локальную подсистему, в которой идут уменьшающие энтропию процессы структурообразования, возникновения упорядоченных форм движения. Например, в результате человеческой деятельности из горных пород созданы строительные материалы и изделия, построены жилые здания и заводы, из добытой руды выплавлены металлы и изготовлены изделия из них. За счет энергии горючих ископаемых или гидроэнергии вырабатывается электроэнергия, которая, в свою очередь, приводит в упорядоченное движение транспортные средства, детали станков и механизмов, отапливает помещения, создавая разность температур между ними и окружающей средой. Но эти снижающие энтропию и увеличивающие порядок процессы возможны лишь потому, что рассматриваемый объект является подсистемой более широкой системы, и неизбежно сопровождаются иными процессами в широкой системе, увеличивающими энтропию и беспорядок системы в целом. Создание строительных изделий, домов, машин (структурирование) перекрывается деструкцией, разрушением создававшихся тысячелетиями природных объектов; а энергия упорядоченных форм движения и взаимодействия (механическая, химическая, электрическая) в конце концов превращается в неупорядоченную - тепловую.

Итак, второе начало термодинамики констатирует деградацию форм движения, взаимодействия, структурной организации материи в изолированных системах. Р. Клаузиус и ряд других исследователей перенесли, экстраполировали этот вывод на всю Вселенную и пришли к выводу о неизбежности выравнивания температур всех тел Вселенной, прекращения всех форм движения, кроме хаотического теплового движения, разрушения всех упорядоченных макроструктур. Клаузиус назвал такое гипотетическое состояние «тепловой смертью» Вселенной.

Однако, такой вывод противоречит наблюдаемым нами на Земле и в обозримой части Вселенной процессам образования и эволюции новых структур - от галактических до микроскопических, возникновению новых форм движения вплоть до высших - биологической и социальной.

Наиболее масштабное и обоснованное опровержение концепции «тепловой смерти» Вселенной связано с учетом нестационарности Вселенной. Дело в том, что однородное изотермическое распределение вещества в нестационарной Вселенной не соответствует максимуму энтропии, то есть наибольшей вероятности. Гравитационные процессы во Вселенной, расширяющейся после Большого Взрыва, приводят к формированию неоднородностей, из которых далее образуются скопления галактик, галактики, звезды и т.д. Именно такой сценарий эволюции Вселенной соответствует возрастанию энтропии и не нарушает законов термодинамики. С учетом релятивистского тяготения он и в будущем не приведет к «тепловой смерти» Вселенной.

Вопросами структурообразования в термодинамически неравновесных локальных системах занимается бурно развивающаяся в последние годы отрасль естествознания - синергетика.