Колебательные процессы. Фурье-анализ

Долгое время в физике изучались лишь механические колебания и волны; им был посвящен один из разделов классической механики. С конца 19-го века начали исследовать электромагнитные колебания и волны. Затем круг рассматриваемых колебательных и волновых процессов разной природы стал расширяться. Кроме физики, колебательные процессы стали изучаться в химии (колебательные реакции), в биологии (колебания численности популяции), в других естественных науках, а также и в общественно-экономических науках (колебания деловой активности, курсов валют). Сейчас теория колебаний и волн из вспомогательного раздела механики развилась в одну из основных физических наук, связанную со всем естествознанием. Методологической основой этой науки является то, что в способах описания, в свойствах и закономерностях колебательных и волновых процессов самой различной природы очень много общего. Наиболее сильно эта общность проявляется для колебаний и волн, относящихся к физической форме движения.

Колебательным процессом (колебанием) называется процесс, обладающий некоторой повторяемостью во времени, то есть процесс, в ходе которого значения какой-либо величины 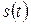повторяются или почти повторяются через равные промежутки времени, называемые периодом колебаний.

Колебательной называется механическая или иная система, в которой после того, как ее вывели из состояния покоя (равновесия) и предоставили самой себе, происходят колебания. Колебания называются свободными или собственными, если на систему после выведения из равновесия внешние воздействия не оказываются. Если же на систему оказывается внешнее периодическое воздействие, то колебания называются вынужденными.

Простейшей, но важнейшей разновидностью колебаний являются гармонические колебания, при которых колеблющаяся величина меняется со временем по закону синуса или косинуса:

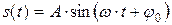, (8.1)

где 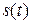- колеблющаяся величина, A - амплитуда колебаний, то есть наибольшее значение величины s, достигаемое в ходе колебаний, 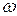- циклическая частота колебаний, t - время, 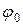- начальная фаза колебаний. Величину 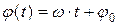называют фазой колебаний.

Кроме того, гармонические (и не только гармонические) колебания характеризуют период T - время, за которое совершается одно полное колебание, и частота 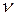- число колебаний за единицу времени.

Величины 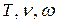взаимосвязаны:

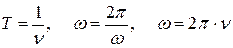. (8.2)

Если система находится под одновременным действием нескольких факторов, вызывающих в ней колебания, то результат их совместного действия зависит от свойств системы. Линейной называется система, свойства которой не изменяются под действием происходящих в ней колебаний. Для такой системы справедлив упоминавшийся в подразделе 5.2 принцип суперпозиции: в каждый момент времени значение колеблющейся величины s равно сумме значений 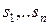, которые эта величина имела бы под действием каждого из факторов, вызывающих колебания, по отдельности.

Система, свойства которой изменяются в результате происходящих в ней колебаний, называется нелинейной и для нее принцип суперпозиции неприменим.

Например, линейным будет резистор, электрическое сопротивление которого не зависит от силы идущего по нему тока. Если к нему приложить переменное напряжение, меняющееся по гармоническому закону, то по нему будет протекать переменный ток (сила тока будет совершать гармонические колебания) с некоторой амплитудой. При увеличении амплитуды приложенного к резистору напряжения в 2, 3, ... n раз амплитуда колебаний силы тока также возрастет в 2, 3, ... n раз. Если же резистор нелинейный, то есть его сопротивление само зависит от силы тока, например, из-за нагрева, то, во-первых, увеличение амплитуды колебаний напряжения не вызовет пропорционального изменения амплитуды колебаний силы тока. Во-вторых, вид зависимости силы тока от времени 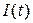будет отличаться от вида зависимости напряжения от времени 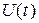. То есть, если колебания напряжения будут гармоническими, то колебания силы тока таковыми не будут.

Говорят, что в линейных системах отклик на внешнее воздействие линейный (пропорциональный воздействию), а в нелинейных системах - отклик нелинейный.

Система будет являться колебательной, если при ее отклонении от положения равновесия в ней возникают силы, стремящиеся вернуть ее в положение равновесия (возвращающие силы). Система будет совершать гармонические колебания в том и только в том случае, если величина возвращающей силы прямо пропорциональна величине отклонения от положения равновесия (квазиупругая возвращающая сила).

В теории колебаний широко используется так называемый Фурье-анализ. Он основан на том, что процесс, обладающий некоторой периодичностью и повторяемостью во времени, может быть представлен как сумма гармонических колебаний. Фурье-анализ позволяет на основе фиксации исследуемого процесса в течение достаточно длительного времени определить амплитуды и периоды составляющих этот процесс гармонических колебаний и на этом основании прогнозировать развитие этого процесса в будущем. Например, изучая в течение многих лет зависимость солнечной активности от времени, обнаружили, что в этой на первый взгляд хаотической зависимости на фоне случайных флуктуаций проявляются колебания с периодом примерно в 11 лет - так называемый «одиннадцатилетний солнечный цикл». Это позволяет предсказывать (естественно, с погрешностью) изменение солнечной активности на ближайшие годы, что представляет интерес с точки зрения медицины и экологии. По-видимому, в солнечной активности проявляются и более долговременные циклы, которые, вероятно, ответственны за изменения климата на Земле. Большой интерес представляет применение этого метода для прогнозирования в области экономики, финансов, социологии.