Системы из большого числа частиц. Статистический и термодинамический методы. Статистические закономерности. Флуктуации

Качественно новые закономерности движения и взаимодействия материи проявляются при изучении систем, состоящих из очень большого числа частиц. К ним относятся окружающие нас макротела в различных агрегатных состояниях: твердом, жидком, газообразном. Даже сравнительно малые тела содержат огромное число частиц: молекул, атомов, ионов, свободных электронов. При обычных давлениях и температуре 1 м³ газа содержит порядка 10²⁵ частиц, а жидкого или твердого тела – порядка 10²⁸ частиц.

Пусть требуется теоретически исследовать какие-то свойства макроскопического тела (упругость, теплоемкость, электропроводность и т.д.) или закономерности каких-либо процессов в нем (зависимость давления от объема при изотермическом процессе, зависимость электропроводности металла от температуры и т.д.). Если действовать в рамках механистической парадигмы, то нужно установить динамические закономерности движения для всех частиц тела, для чего записать уравнения их движения, решить полученную систему уравнений с учетом начальных условий и связать состояния всех частиц с макроскопическими характеристиками тела: давлением, теплоемкостью, электропроводностью и проч. Очевидно, что не только решить эту задачу в полном объеме, но даже записать все исходные уравнения движения совершенно невозможно. Но этого и не требуется, поскольку, очевидно, макроскопические свойства тела очень мало зависят от состояния той или иной отдельной частицы, но связаны с обобщенными (усредненными) характеристиками движения и взаимодействия всех частиц тела.

То же самое можно сказать и о химических свойствах систем, состоящих из большого числа частиц, о свойствах биологическим систем, состоящих из множества особей, социальных систем, состоящих из множества индивидуумов.

Физические свойства макроскопических систем, содержащих очень большое число частиц, изучаются двумя взаимно дополняющими друг друга методами: статистическим и термодинамическим. Статистический метод (статистическая физика) основан на том, что, хотя координаты и импульсы (и другие параметры) отдельных частиц (элементов системы) являются случайными величинами, тем не менее, в совокупном поведении большого числа частиц проявляются особые, так называемые статистические закономерности. В отличие от динамических, статистические закономерности позволяют на основании информации о состоянии объекта в некоторый момент и о воздействиях на этот объект предсказать лишь вероятность того или иного состояния объекта в последующие моменты времени. Поскольку фактор случайности в принципе неустраним (хотя в некоторых случаях им можно пренебречь), то статистические закономерности имеют более общий характер, чем динамические. Математический аппарат статистического метода базируется на теории вероятностей и математической статистике.

Например, хотя координаты отдельных частиц газа являются случайными, но в среднем в сосуде небольшого объема частицы распределяются по сосуду примерно равномерно. В большом объеме газа, находящегося в поле силы тяжести, например, в земной атмосфере, концентрация частиц с высотой изменяется, но подчиняется определенной закономерности (распределению Больцмана). Скорости частиц газа также являются случайными величинами, но при фиксированной температуре в газе устанавливается стационарное распределение частиц по скоростям (распределение Максвелла), то есть каждому диапазону скоростей (от 0 до 1 м/с, от 1 м/с до 2 м/с и т.д.) соответствует определенная, почти постоянная во времени доля частиц.

Отличительной особенностью величин, описываемых статистически, является неизбежность флуктуаций, то есть хаотически изменяющихся незначительных отклонений значений этих величин в ту или иную сторону от средних значений. Так, в приведенном выше примере с равномерным распределением частиц в сосуде постоянна по объему и во времени лишь средняя концентрация частиц, а локальные (местные) значения концентрации все время хаотически колеблются около этого среднего значения. Так же и в примере с распределением частиц газа по скоростям: доля частиц, скорости которых лежат в определенном диапазоне, все время и во всех частях объема газа незначительно изменяется, но среднее по объему и по времени значение этой величины постоянно.

Многие макроскопические свойства тел определяются средними значениями характеристик движения и взаимодействия частиц. Давление идеального газа связано со средней энергией поступательного хаотического движения частиц, о чем свидетельствует основное уравнение молекулярно-кинетической теории идеального газа, известное из школьного курса физики. С той же средней энергий связана и абсолютная температура среды. Теплопроводность газов пропорциональна средней скорости хаотического теплового движения частиц газа и средней длине свободного пробега частиц между двумя столкновениями; с ними же, но иначе, связано удельное электрическое сопротивление металлов (в последнем случае под частицами подразумеваются свободные электроны).

Некоторые же макроскопические свойства тел обуславливаются флуктуациями параметров. Например, голубой цвет неба объясняется рассеянием света с малой длиной волны на флуктуациях плотности воздуха, то есть случайных локальных, изменяющихся со временем отклонениях концентрации частиц воздуха от среднего значения.

При переходе от изучения простых систем к более сложным роль статистических методов возрастает. Они широко используются в квантовой физике и при исследованиях биологических и социальных систем.

Принципиальным отличием статистических закономерностей от динамических является переход от детерминизма динамических закономерностей к вероятностному характеру статистических и допущение неизбежности флуктуаций - хаотических отклонений локальных значений параметров от средних значений.

Как будет показано далее, еще одним отличием систем из большого числа частиц от простейших механических является необратимость во времени протекающих в них процессов, наличие определенного направления развития в сложных системах.

Кроме статистического метода, для исследования свойств макроскопических систем и различных явлений в них служит термодинамический метод, основанный на анализе процессов передачи и превращений энергии, происходящих в системе. Соответствующий раздел физики называется термодинамикой. В термодинамике внутреннее строение тел, движение и взаимодействие их частиц не рассматриваются. Замечательной особенностью термодинамики является то, что установленные ею законы справедливы для самых разнообразных систем вне зависимости от их внутреннего строения.

Термодинамика базируется на небольшом количестве основных законов (начал), надежно установленных опытным путем. Наиболее широко используются первое и второе начала термодинамики; в ряде задач используется третье начало - тепловая теорема В. Нернста. Утверждение о существовании температуры - параметра, единого для всех частей термодинамически равновесной системы, - называют иногда нулевым началом термодинамики. Приведем определения ряда терминов, базовых для термодинамики и широко применяемых в других отраслях естествознания.

Термодинамическая система - мысленно выделенная совокупность макроскопических тел, могущих взаимодействовать, обмениваться энергией и веществом друг с другом и с внешними телами.

Открытой называется система, могущая обмениваться веществом и энергией с окружающей средой. Типичные примеры открытых систем - все живые организмы, другой пример - жидкость, масса которой может изменяться вследствие испарения, кипения или конденсации.

Закрытая система не может обмениваться веществом с окружающей средой.

Изолированная система не может обмениваться с окружающей средой ни веществом, ни энергией.

Замкнутая система изолирована в механическом отношении, то есть не обменивается энергией с внешней средой путем совершения работы.

Адиабатная система не обменивается энергией с внешней средой путем теплообмена.

Состояние механической системы, как говорилось выше, характеризуют координаты и скорости (или импульсы) всех частиц системы. Такое описание системы многих частиц невозможно. Поэтому состояние термодинамической системы макроскопических тел характеризуют качественно иные параметры, называемые термодинамическими параметрами: температура, объем, давление, концентрация и др.

Термодинамические параметры принципиально отличаются от механических характеристик состояния тем, что они описывают качества, возникающие только у систем из большого количества частиц, которых не может быть у отдельных частиц. Действительно, говорить о температуре, давлении, вязкости, электропроводности и т.п. применительно к одной материальной точке или к системе из немногих частиц бессмысленно. Точно так же системы из множества молекул, сообщества живых организмов, индивидуумов проявляют качества, которых нет у отдельных членов таких систем, и для описания которых в химии, биологии, социологии используются параметры, неприменимые для отдельных элементов систем.

Равновесным называется состояние, в которое при неизменных внешних условиях приходит предоставленная самой себе термодинамическая система и в котором затем остается сколь угодно долго. В состоянии равновесия параметры системы не изменяются со временем (однако возможны флуктуации). При этом ряд параметров (обязательно - температура, в отсутствие внешних силовых полей - давление, и ряд прочих) одинаковы по всему объему системы; в системе отсутствуют потоки (например, потоки вещества или энергии, электрический ток).

Представим неравномерно нагретое тело. Ему нельзя приписать определенное значение температуры, но если его изолировать от внешней среды и предоставить самому себе, то температура выровняется и примет одинаковое для всех точек значение - тело перейдет в равновесное состояние.

Неравновесным называется состояние системы, выведенной из равновесного состояния. Процесс самопроизвольного перехода изолированной системы из неравновесного состояния в равновесное называется релаксацией. Время, за которое отклонение какого-нибудь параметра от его равновесного значения уменьшается в е раз ( 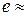2.72), называется временем релаксации данного параметра.

Термодинамическим процессом называется всякое изменение состояния термодинамической системы, ведущее к изменению ее параметров.

Процесс называется равновесным, если в ходе этого процесса система проходит непрерывный ряд бесконечно близких термодинамически равновесных состояний. Например, процесс сжатия газа можно считать равновесным, если в каждый момент этого процесса давление и другие параметры газа одинаковы по всему объему. Очевидно, чтобы процесс был равновесным, необходимо, чтобы он протекал бесконечно медленно (квазистатически). Реальные процессы происходят за конечное время и, строго говоря, равновесными не являются. Однако реальный процесс с достаточной степенью точности можно считать равновесным, если его длительность во много раз больше времен релаксации всех параметров системы.

Для неравновесных процессов нельзя говорить об единых для всей системы значениях параметров: давления в быстро сжимаемом газе, температуры тела, нагреваемого с одной стороны, и т.д. То же в некоторых случаях справедливо и для равновесных процессов и состояний. Например, для равновесной земной атмосферы нельзя указать одинаковое для всех высот давление. В таких случаях (для неравновесных процессов и равновесных состояний с непостоянными в пространстве параметрами) тело мысленно разбивают на малые области и говорят о локальном (местном) значении параметров. Говорить о температуре предмета, нагреваемого с одной стороны, бессмысленно, но можно говорить о локальной температуре различных физически малых объемов этого тела.

Поскольку определение значений многих параметров для тела как целого в неравновесных процессах теряет смысл, то становится невозможным и установление законов, связывающих такие параметры, а также построение графиков зависимости этих параметров от времени или друг от друга. Эти обычные для исследователя способы описания в случае термодинамически неравновесных процессов применимы только по отношению к локальным значениям параметров.

Однако многие реальные процессы осуществляются достаточно медленно, чтобы их с приемлемой точностью можно было считать равновесными. Примерами равновесных термодинамических процессов являются известные из школьного курса физики изопроцессы, адиабатный процесс.

Обратимым называется процесс, допускающий возможность возвращения системы в первоначальное состояние через ту же последовательность промежуточных состояний, что и в прямом процессе, но проходимых в обратном порядке.

Иначе говоря, процесс называется обратимым, если после него можно возвратить саму систему и все взаимодействующие с ней тела в их начальное состояние так, чтобы в них не возникло никаких остаточных изменений. В противоположном случае процесс называется необратимым.

Всякий обратимый процесс является равновесным, но не всякий равновесный процесс обратим. Равномерное движение тела по шероховатой поверхности под действием взаимно уравновешивающихся сил тяги и трения - процесс равновесный, но необратимый.

Вторая половина 19-го века - начало 20-го века - период быстрого развития классической статистической физики и термодинамики, изучавших системы из большого числа классических (неквантовых) частиц в равновесном или близком к равновесному состояниях. Этот этап связан с именами Дж. Максвелла (англ.), Л. Больцмана (австр.), С. Карно (фр.), Р. Клаузиуса (герм.), Дж. Гиббса (амер.) и др.

В 20-ом веке получила развитие квантовая статистика, изучающая системы частиц, подчиняющихся не классической, а квантовой механике (А. Эйнштейн, Ш. Бозе (инд.), Э. Ферми (итал.), П. Дирак (англ.), Л. Бриллюэн (фр.), И.Е. Тамм, Я.И. Френкель, Л.Д. Ландау (сов.)) и термодинамика неравновесных процессов (Л. Онсагер (амер.), И.Р. Пригожин (бельг.)).