Связь законов сохранения с симметрий пространства-времени. Устойчивость механического равновесия и движения. Обратимость механических процессов. «Стрела Времени»

К симметрийным свойствам пространства-времени относятся однородность и изотропность пространства и однородность времени. С каждым из этих трех свойств связан один из трех рассмотренных законов сохранения.

Покажем, что закон сохранения импульса связан с однородностью пространства. В подразделе 6.2 при выводе закона сохранения импульса использовались все три закона Ньютона. Третий закон применялся при доказательстве того, что сумма внутренних сил равна нулю. Оказывается, что достаточно первых двух законов, а равенство нулю суммы внутренних сил следует из однородности пространства.

Действительно, однородность пространства означает, что законы движения и физические свойства замкнутой системы не зависят от выбора начала координат инерциальной системы отсчета. Иначе говоря, они не изменятся, если замкнутую систему переставить в пространстве как целое путем параллельного переноса всех частиц системы при сохранении их взаимного расположения и условий, в которых они находились до переноса.

В частности, при произвольном малом перемещении 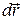системы двух точек как целого, работа 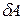всех сил в системе должна быть равна нулю, иначе в системе произошли бы превращения энергии. В замкнутой системе работают лишь внутренние силы, так что

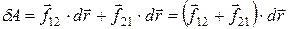. (6.26)

Так как 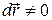, то сумма внутренних сил .

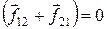Из последнего соотношения, уравнений (6.3), выражающих второй закон Ньютона, и условия замкнутости системы (все внешние силы равны нулю) и вытекает закон сохранения импульса.

Аналогично можно показать, что закон сохранения момента импульса связан с изотропностью пространства, то есть одинаковостью его свойств по всем направлениям. Иначе говоря, изотропность пространства означает, что законы движения и физические свойства замкнутой системы не изменяются при ее повороте как целого в пространстве на произвольный угол.

Наконец, закон сохранения механической энергии связан с однородностью времени, то есть его независимостью от выбора начала отсчета. Иначе говоря, однородность времени означает, что если две идентичные системы поставить в одинаковые условия в два разных момента времени, то, начиная с этих моментов, все процессы в системах будут происходить одинаково.

Представления о симметрии и ее связи с законами сохранения получили успешное развитие в теории элементарных частиц и фундаментальных физических взаимодействий. Понятие симметрии также используется в химии и биологии.

Равновесие механической системы - состояние, когда все точки системы под действием приложенных к ним сил остаются неподвижными относительно выбранной системы отсчета.

Движение и равновесие механической системы могут быть устойчивыми и неустойчивыми.

Движение называется устойчивым, если после малого силового внешнего воздействия на частицы системы (возмущения) во все последующие моменты состояния системы будут мало отличаться от состояний в отсутствие возмущения. Если же сколь угодно малое внешнее воздействие вызовет нарастающее изменение состояний системы по сравнению с невозмущенным движением, то такое движение - неустойчивое.

Рассмотрим качение шарика по горизонтальному цилиндру (рисунок 6.4). Движение шарика по внутренней поверхности вдоль линии KL устойчиво, так как малые внешние воздействия вызовут лишь малые изменения характера движения. Движение же шарика по внешней поверхности вдоль линии AB неустойчиво, так как сколь угодно малый толчок в боковом направлении вызовет нарастающее изменение движения.

Рисунок 6.4 - К определению устойчивости движения.

Равновесие устойчиво, если после малого смещения все точки системы все последующее время мало отклоняются от положения равновесия; в противном случае механическое равновесие неустойчиво.

Условие механического равновесия связано с механической энергией системы. Консервативные силы направлены так, что стремятся привести систему в состояние с наименьшей потенциальной энергией. Отсюда следует, что равновесие механической системы устойчиво, если ему соответствует минимум потенциальной энергии. Так, в поле силы тяжести равновесие шарика, лежащего в нижней точке полусферической чаши, направленной выпуклостью вниз, устойчиво, так как ему соответствует наинизшее возможное положение и минимум потенциальной энергии. Равновесие же шарика, лежащего на вершине полусферического купола, неустойчиво, так как ему соответствует максимум потенциальной энергии.

В заключение затронем вопрос об обратимости механических процессов.

Рассмотрим систему материальных точек (частиц), между которыми действуют гравитационные силы, а также - при наличии у частиц электрических зарядов - силы электромагнитной природы: сила Кулона и сила Лоренца. Гравитационные силы и силы Кулона зависят от расположения частиц в пространстве, а сила Лоренца - также от скоростей движения частиц.

Если изменить в какой-то момент времени скорости всех частиц на противоположные, то система будет проходить все предыдущие состояния в обратном порядке, то есть время как бы пойдет вспять. Это свойство механических процессов называется их обратимостью во времени. Обратимость механических процессов обусловлена симметрией (неизменностью) основного закона классической механики - второго закона Ньютона - относительно замены переменной t на -t.

Учет сильного и слабого взаимодействий частиц не изменяет вывод об обратимости механических процессов в системе частиц.

В системе макроскопических тел механические процессы обратимы во времени только при условии, что в системе действуют лишь стационарные консервативные силы, то есть выполняется закон сохранения механической энергии и, следовательно, отсутствуют превращения механической энергии в другие виды энергии и наоборот.

Но в реальных макроскопических системах действуют и неконсервативные силы, например, сила трения. Сила трения, как и силы Кулона и Лоренца, также имеет электромагнитную природу, но обусловлена коллективным взаимодействием огромного количества частиц соприкасающихся тел. Если неконсервативные силы совершают работу, то механический процесс является необратимым. Достаточно представить себе колебания маятника в вязкой среде. Эти колебания затухают, и изменение направления движения маятника в какой-либо момент на противоположное не приведет к обратному процессу нарастания размаха колебаний.

Таким образом, имеется явное противоречие между обратимостью во времени уравнений динамики систем материальных частиц и необратимостью реальных процессов в макроскопических системах. Иначе говоря, с точки зрения классической механики оба направления развития материального мира во времени - реальное и обратное – равноценны, и выбор одного из них случаен. Но это не согласуется с повсеместно наблюдающейся в окружающем мире тенденцией к развитию от простого к сложному, возникновению новых, ранее не существовавших в природе, материальных структур (от звездных систем до живых организмов). Такую необратимость развития мира, однонаправленность образно называют «стрелой Времени».

Разрешение этого противоречия, выявление причин необратимости развития материального мира является одной из фундаментальных проблем современного естествознания.