Функции распределения случайных величин

Остановимся на некоторых важнейших, концептуальных результатах, полученных одним из разделов классической статистической физики - молекулярно-кинетической теорией (МКТ) строения вещества.

Во-первых, МКТ выяснила статистический смысл понятия температуры, которая долгое время трактовалась как эмпирическая мера нагретости вещества.

Основное уравнение МКТ идеального газа получено теоретически путем вычисления средней силы воздействия на стенки сосуда, возникающей вследствие абсолютно упругих соударений хаотически движущихся частиц газа со стенками. Оно связывает давление p с концентрацией n частиц (их числом в единице объема) и средней кинетической энергией 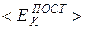их поступательного движения:

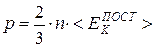. (7.1)

Путем обобщения опытных данных было получено уравнение состояния идеального газа (уравнение Менделеева - Клапейрона):

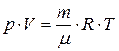. (7.2)

где V - объем газа; m - его масса; 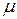- молярная масса; T – абсолютная температура; R=8,31 Дж/(моль·К) - универсальная газовая постоянная.

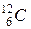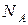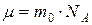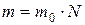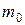Учтем, что моль - это количество вещества, которое содержит столько же частиц (молекул, атомов, ионов), сколько атомов содержат 12 г изотопа углерода . Количество частиц в моле – число Авогадро =6.02·10²³ 1/моль. Представим молярную массу в виде , а массу газа , где - масса одной частицы, N - полное их число в газе.

Подставим эти выражения в уравнение (7.2) и, учитывая, что концентрация частиц 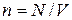, сведем (7.2) к виду:

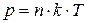, (7.3)

где 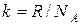=1.38·10^-23 Дж/К - константа, называемая постоянной Больцмана.

Сопоставление уравнения (7.1), полученного теоретически, и уравнения (7.3), полученного на основе опыта, приводит к соотношениям

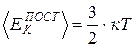, (7.4)

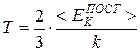, (7.5)

из которых следует, что со статистической точки зрения абсолютная температура есть мера средней энергии хаотического теплового движения частиц среды, находящейся в состоянии термодинамического равновесия.

Другим важнейшим результатом классической статистической физики стало установление статистических закономерностей распределения частиц в равновесных системах, состоящих из большого числа частиц, по скоростям и энергиям. Такие статистические закономерности описываются с помощью функций распределения случайных величин. Функции распределения случайных величин изучаются в математической статистике и широко применяются для описания самых разнообразных систем (коллективов), состоящих из большого числа частиц (членов). Они находят применение во всех отраслях естествознания, в экономике и социологии.

Пусть некоторая величина x может случайным образом принимать различные значения в пределах своей области определения. Примеры таких величин: в статистической физике - скорость или кинетическая энергия частицы газа, в измерительной технике - результаты серии измерений любой величины, при которых имелись случайные погрешности. При исследованиях больших коллективов людей - возраст, вес, ежемесячный доход каждого человека. Пусть имеется очень большое количество N значений этой случайной величины: скоростей N молекул, результатов N измерений, данных о доходе N человек. Некоторые из этих значений могут совпадать. Обозначим через 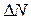количество значений случайной величины, лежащих в пределах от x до 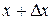. Например, 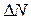- число частиц газа, у которых скорости в данный момент лежат в пределах от 100 м/с до 120 м/с. Тогда отношение 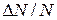есть вероятность того, что взятое наугад значение случайной величины лежит в промежутке от x до 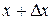. Отношение 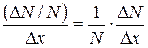показывает, какова вероятность того, что некоторое значение случайной величины лежит в единичным промежутке изменения x. Подобно тому, как масса веревки, отнесенная к ее длине, дает среднюю линейную (погонную) плотность веревки, так и отношение вероятности 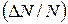к ширине 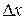промежутка дает среднюю плотность вероятности на этом промежутке. Чтобы определить не усредненное, а истинное значение плотности вероятности при некотором значении x, нужно перейти к пределу при :

.

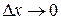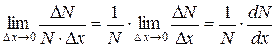Полученное выражение и определяет функцию распределения 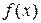случайной величины:

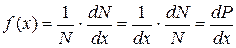, (7.6)

где 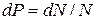есть вероятность попадания случайной величины в бесконечно малый промежуток от x до .

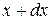Таким образом, функция распределения 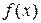(в математической статистике - дифференциальная функция распределения) есть плотность вероятности попадания значения случайной величины в малый промежуток от x до .

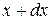Если известен вид функции распределения 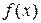, то вероятность dP может быть найдена из формулы (7.6):

,

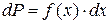следовательно, вероятность 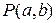того, что значение случайной величины x лежит в промежутке от a до b, определяется интегралом

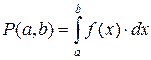, (7.7)

причем промежуток от a до b должен принадлежать области определения случайной величины x.

Интеграл (7.7) по всей области определения величины x ( 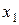и 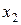- границы этой области) равен единице:

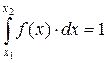, (7.8)

так как вероятность того, что случайная величина принимает хотя бы какое-то значение в области своего определения, очевидно, равна 1 (то есть 100%).

В 1859 г. Дж. Максвелл установил вид функции распределения частиц газа по абсолютным значениям (модулям) скорости:

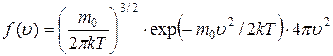, (7.9)

где 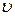- модуль скорости частицы газа (область определения: 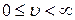), - масса частицы газа.

График функции распределения Максвелла показан на рисунке 7.2а, где две кривые соответствуют двум различным температурам газа. Из этих графиков видно, что вероятность того, что частица имеет очень малую скорость ( 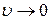) или очень большую скорость ( 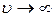), невелика, а основная доля частиц газа имеет скорости, близкие к наиболее вероятной скорости .

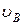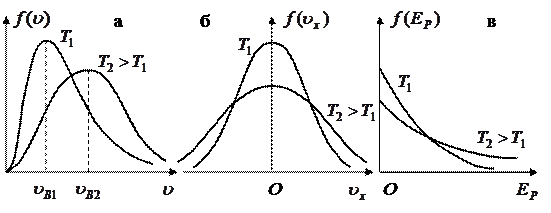
Рисунок 7.2. Графики функций распределения Максвелла (а), Гаусса (б) и Больцмана (в).

Если в качестве случайной величины рассматривать не модуль скорости, а ее проекцию на какую-либо координатную ось, например 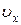, то ее область определения: 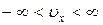, а распределение частиц газа по проекциям скорости описывается распределением Гаусса:

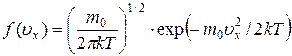. (7.10)

График распределения частиц газа по проекциям скорости показан на рисунке 7.2б. Ввиду широкой распространенности гауссовского закона распределения случайных величин его называют также нормальным законом распределения.

Если газ находится в поле консервативных сил, то потенциальная энергия его частиц в разных точках пространства различна. Как уже указывалось, в механических системах консервативные силы стремятся переместить частицы в положение, в котором их потенциальная энергия минимальна. Но в системах из множества малых частиц этому препятствует хаотическое тепловое движение, стремящееся «разбросать» частицы по пространству. Сказанное иллюстрирует пример земной атмосферы. Силы тяжести стремятся опустить все частицы воздуха на поверхность Земли, но их хаотическое тепловое движение этому препятствует. В результате действия этих противоположных тенденций в термодинамически равновесной системе устанавливается распределение частиц по потенциальным энергиям, вид которого в 1886 г. установил Л. Больцман (см. рисунок 7.2в):

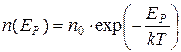, (7.11)

где 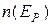- концентрация частиц в той точке, где потенциальная энергия частицы равна 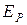, 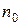- концентрация частиц там, где их потенциальная энергия равна нулю. Из формулы (7.11) видно, что концентрация частиц экспоненциально уменьшается с ростом их потенциальной энергии. Поскольку потенциальная энергия частиц воздуха пропорциональна высоте 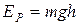, то из (7.11) следует, что в изотермической ( 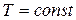) атмосфере концентрация частиц и, следовательно, давление (см. формулу (7.3)), экспоненциально уменьшается с ростом высоты.

Все указанные распределения верны для так называемых классических частиц, движение которых описывается классической механикой. Распределения квантовых частиц, движение которых подчиняется законам квантовой механики, иные; о них речь пойдет в следующих разделах.