Автоматические регуляторы и законы регулирования

3.3.1. Классификация линейных регуляторов

По функциональному назначению и конструктивномуисполнению

регуляторы можно квалифицировать следующим образом:

1. По виду регулируемой величины: регуляторы температуры, давления, уровня, влажности и т. д.

2. Регуляторы прямого и непрямого действия: в регуляторах прямого дейст­вия измерительное устройство без дополнительного источника энергии непосредственно воздействует на регулируемый орган, через который проходит в объект вещество или энергия; в регуляторах непрямого действия имеется блок усиления и преобразования, который питается от дополнительного источника энер­гии и усиливает мощность выходного сигнала до величины, способной управлять мощными регулирующими органами с большими потоками вещества и энергии.

3. В зависимости от рода вспомогательной энергии различают регуляторы электрические, пневматические, гидравлические и комбинированные (на­пример, электропневматические и др.).

В большинстве случаев предпочтение отдается электрическим регуляторам благо­даря компактности, малой массе, небольшим габаритам, возможности управлять на больших расстояниях, широкими возможностями усиления и преобразования сиг­налов.

В тех случаях, когда требуются большие усилия и моменты для привода ра­бочих органов, и необходимо соблюдать условия взрыво- пожаро-безопасности применяют гидравлические или пневматические регуляторы, обладающие высокой надежностью в работе и сравнительной простотой в обслуживании. Однако по­требность в больших сетях трубопроводов, необходимость иметь насосные и компрессорные станции значительно усложняет автоматическую систему при использовании таких регуля­торов. Распространенными являются комбинированные регуляторы, в которых измерительная часть – электрическая, а исполнительный элемент – гид­равлический или пневматический.

4. По функциональной зависимости между регулирующим воздействием у( t ) и отклонением регулируемой величины от заданного значения ∆ (t)

у (t) = f (Δ(t)),

различаются регуляторы, работающие по определенным типовым законам. Уравне­ния, определяющие закон регулирования, могут быть линейными и нелинейными. Часто на практике уравнения регуляторов упрощают, пренебрегая нелинейностями, когда это возможно.

Для АСР, действующих по отклонению регулируемой величины от задан­ного значения, закон регулирования в общем виде записывается так

y( t ) = F·[Δ(t) ]. (3.6) Первая часть выражения (3.6) может содержать не только ошибку Δ, но и ее производные и интегралы. Производные и интегралы вводятся в закон регулиро­вания для улучшения свойств АСР - повышение устойчивости, точности и качества процесса регулирования.

Рассмотрим выражение(3.6) применительно к типовым законам регулирова­ния.

Пропорциональный закон регулирования(П-регулятор) – простейший регу­лятор, в котором регулирующее воздействие у(t) зависит только от ошибки Δ(t)

у(t) = К_Р·Δt, или у = К_Р·Δ, (3.7)

где К_Р называется коэффициентом усиления регулятора.

В промышленных регуляторах предусмотрена возможность изменения К_Р и поэтому он является параметром настройки регулятора. Изменяя К_Р, мы изменяем величину регулирующего воздействия, соответствующую одной и той же ошибке Δ(t). Достоинства регулятора – его простота. Недостатки – регулятор не может полностью ликвидировать ошибку.

Интегральный закон регулирования (И-регулятор). Статическую ошибку можно исключить, если использовать интегральный закон регулирования

у = К_И ∫ Δ dt (3.8)

Коэффициент К_И = 1/Т_И, где Т_И- параметр настройки регулятора, называемый по­стоянной времени интегрирования

Недостаток регулятора: динамические свойства хуже, чем у П-регулятора, т. е. процесс регулирования отстает от процесса появления и изменения отклонения, что приводит (рис.3.5.) к слабо затухающим колебаниям регулируемой величины около заданного x_ЗАДее значения (удлиняется время регулирования).

Пропорционально-интегральный закон регулирования(ПИ-регулятор). Устранить недостаток и сохранить преимущества пропорционального и интеграль­ного регуляторов позволяет регулятор, обеспечивающий закон регулирования:

У = К_Р · ( Δ + 1 /Т_И ∫ Δ·dt ), (3.9)

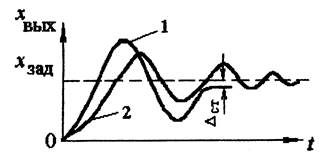
Рис. 3.5. Характер изменения регулируемой величины (х_ВЫХ)

в П-регуляторах (кривая 1) и в И-регуляторах (кривая 2 )

Как видно, ПИ-регулятор имеет два параметра настройки – К_Р и Т_И. Параметр Т_И характерезует интенсивность ввода интеграла в закон регулирования.

Пропорционально-дифференциальныйзакон регулирования(ПД-регулятор). Введение в закон регулирования производной отклонения регулируемой величины улучшает динамические свойства АСР,

y = К_Р ∙ (Δ + T _Д ∙ d Δ/dt). (3.10)

Регулятор имеет два параметра настройки – К_Р и Т_Д.. Коэффициент Т_Д называется временем дифференцирования, или временем предварения, т.к. наличие производной в законе регулирования обуславливает реакцию не только на саму ошибку Δ, но и на тенденцию ее изменения, как бы предвидя развитие событий.

Пропорционально – интегрально - дифференциальный закон регулирования (ПИД-регулятор) описывается уравнением

y = К_Р · ( Δ + 1 /Т_И ∫ Δ·dt + T _Д ∙ d Δ/dt) . (3.11)

Наличие трех составляющих в законе регулироврания (3.11) позволяет добиваться высокого качества процесса регулирования как при установившемся режиме, так и при неустановившихся режимах работы АСР.

Выше рассмотренные законы регулирования являются наиболее простыми, линейными и непрерывными. Для более сложных АСР, например, комбинированных, применяются регуляторы, закон регулирования которых содержит в правой части слагаемые, зависящие от измеряемого возмущения

f (t), его интегралов и производных.

3.3.2. Нелинейные законы регулирования

Наиболее распространенными среди этих законов являются релейные законы, при этом наиболее часто применяется двухпозиционный релейный закон регулирования. В этом случае регулирующий орган может занимать два фиксированных положения (позиции), соответствующее двум фиксированным значениям регулирующего воздействия, вырабатываемого релейным двухпозиционными регуляторами (Рп-регуляторами).