Поток векторного поля. Формула Гаусса-Остроградского
Пусть в области 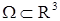 задано некоторое векторное поле
задано некоторое векторное поле 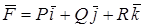 , где
, где 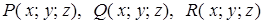 – непрерывно дифференцируемые в области
– непрерывно дифференцируемые в области 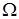 функции. Пусть
функции. Пусть 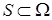 – гладкая ориентированная поверхность, на которой выбрана одна из сторон, задаваемая единичным вектором нормали*
– гладкая ориентированная поверхность, на которой выбрана одна из сторон, задаваемая единичным вектором нормали*  (
( 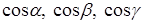 –направляющие косинусы этого вектора).
–направляющие косинусы этого вектора).
Потоком векторного поля 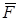 через поверхность
через поверхность 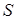 называется поверхностный интеграл
называется поверхностный интеграл
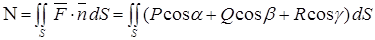 . (4.16)
. (4.16)
Поверхностный интеграл 1-го рода в формуле (4.16) может быть выражен через поверхностный интеграл 2-го рода:
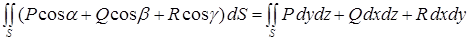 , (4.17)
, (4.17)
что дает еще один способ вычисления потока.
Понятие потока вектора взято из гидродинамики. В гидродинамике рассматривается векторное поле скорости текущей жидкости 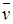 . Поток
. Поток 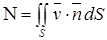 этого векторного поля дает объем жидкости, протекающей через поверхность
этого векторного поля дает объем жидкости, протекающей через поверхность 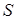 за единицу времени.
за единицу времени.
Если 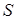 – замкнутая поверхность, являющаяся границей тела
– замкнутая поверхность, являющаяся границей тела 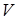 , то имеет место формула Гаусса – Остроградского:
, то имеет место формула Гаусса – Остроградского:
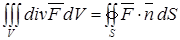 , (4.18)
, (4.18)
(интеграл от дивергенции векторного поля 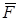 по некоторому объему
по некоторому объему 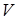 равен потоку этого поля через поверхность
равен потоку этого поля через поверхность 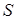 , ограничивающую данный
, ограничивающую данный
объем). Эта формула часто используется для вычисления потока векторного поля через замкнутую поверхность.
*) Нормаль к поверхности в некоторой ее точке 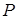 – прямая, проходящая через
– прямая, проходящая через 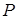 и перпендикулярная к касательной плоскости в этой точке.
и перпендикулярная к касательной плоскости в этой точке.
Формула Гаусса – Остроградского позволяет выразить 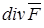 следующей формулой:
следующей формулой:
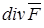 =
= 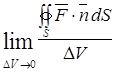 , (4.19)
, (4.19)
которую правильнее всего и считать определением понятия дивергенция: дивергенция вектора 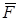 в данной точке поля есть предел, к которому стремится отношение потока вектора
в данной точке поля есть предел, к которому стремится отношение потока вектора 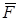 через произвольную, окружающую эту точку, поверхность к величине ограниченного этой поверхностью объема
через произвольную, окружающую эту точку, поверхность к величине ограниченного этой поверхностью объема 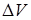 (при
(при 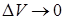 ).
).
Формула (4.19), определяющая дивергенцию, в гидродинамике имеет непосредственный физический смысл: дивергенция скорости 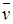 жидкости
жидкости 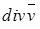 =
= 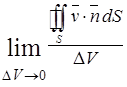 равна рассчитанному на единицу объема количеству жидкости, вытекающей в единицу времени из элемента объема
равна рассчитанному на единицу объема количеству жидкости, вытекающей в единицу времени из элемента объема 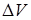 , окружающего рассматриваемую точку. Название «дивергенция», что значит по-латыни расхождение или расходимость, было выбрано для этой величины именно потому, что жидкость растекается или расходится из тех и только из тех точек или участков занимаемого ею пространства, в которых
, окружающего рассматриваемую точку. Название «дивергенция», что значит по-латыни расхождение или расходимость, было выбрано для этой величины именно потому, что жидкость растекается или расходится из тех и только из тех точек или участков занимаемого ею пространства, в которых 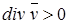 .Очевидно, что в этих точках должны быть расположены источники жидкости. По аналогии, те точки произвольного векторного поля
.Очевидно, что в этих точках должны быть расположены источники жидкости. По аналогии, те точки произвольного векторного поля 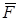 , в которых
, в которых 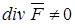 , принято называть истоками этого поля. Численная же величина
, принято называть истоками этого поля. Численная же величина 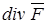 называется силой, или обильностью, истоков поля; в зависимости от знака дивергенции сила истоков может быть как положительной, так и отрицательной. Иногда отрицательным истокам поля дают название стоков поля. Векторные поля, у которых
называется силой, или обильностью, истоков поля; в зависимости от знака дивергенции сила истоков может быть как положительной, так и отрицательной. Иногда отрицательным истокам поля дают название стоков поля. Векторные поля, у которых 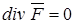 , называются свободными от источников, или соленоидальными (трубчатыми).
, называются свободными от источников, или соленоидальными (трубчатыми).
Пример. Вычислить поток векторного поля 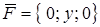 через часть плоскости, заданной уравнением
через часть плоскости, заданной уравнением 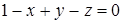 , расположенную в октанте
, расположенную в октанте 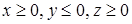 , если единичный вектор нормали
, если единичный вектор нормали 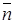 к рассматриваемой поверхности образует острый угол с осью
к рассматриваемой поверхности образует острый угол с осью 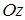 .
.
◄ Вычислим поток 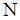 при помощи формулы (4.17). Учитывая, что для данного векторного поля
при помощи формулы (4.17). Учитывая, что для данного векторного поля  , будем иметь
, будем иметь  . Последний интеграл вычислим сведением его к двойному по области
. Последний интеграл вычислим сведением его к двойному по области 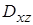 (рис.2), являющуюся проекцией поверхности на плоскость
(рис.2), являющуюся проекцией поверхности на плоскость 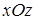 . Так как единичная нормаль образует с осью
. Так как единичная нормаль образует с осью 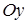 тупой угол (это очевидно из рис. 2) и, следовательно,
тупой угол (это очевидно из рис. 2) и, следовательно,  , перед двойным интегралом необходимо
, перед двойным интегралом необходимо
|
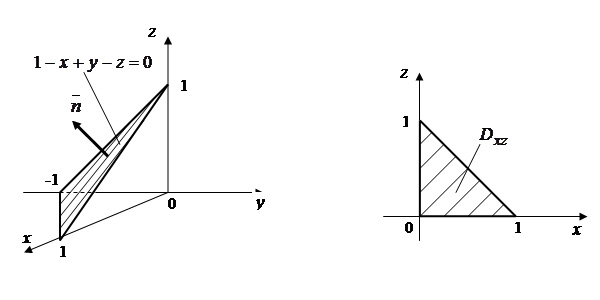
поставить знак минус:  =
= 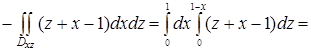
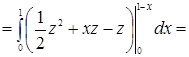
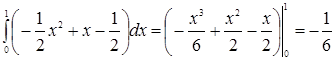 . ►
. ►
Пример. Положительный электрический заряд 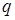 , помещенный в начале координат, создает векторное поле, напряженность
, помещенный в начале координат, создает векторное поле, напряженность 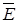 которого в каждой точке пространства определяется законом Кулона:
которого в каждой точке пространства определяется законом Кулона: 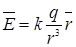 , где
, где 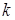 – постоянный коэффициент, величина которого зависит от выбора системы единиц измерения,
– постоянный коэффициент, величина которого зависит от выбора системы единиц измерения, 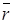 – радиус-вектор точки пространства. Найти поток этого векторного поля через сферу радиуса
– радиус-вектор точки пространства. Найти поток этого векторного поля через сферу радиуса 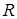 с центром в начале координат.
с центром в начале координат.
◄ Так как 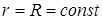 , будем иметь
, будем иметь 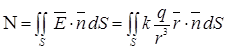 =
=
= 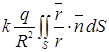 . Скалярное произведение
. Скалярное произведение 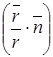 в последнем интеграле равно 1, т. к. единичные векторы
в последнем интеграле равно 1, т. к. единичные векторы  и
и 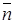 в каждой точке сферы совпадают. Следовательно,
в каждой точке сферы совпадают. Следовательно,  (площадь поверхности
(площадь поверхности 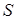 (сферы)). Окончательно, поток
(сферы)). Окончательно, поток 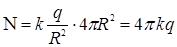 . ►
. ►
Дата добавления: 2016-07-27; просмотров: 11040;











