Потенциальные и соленоидальные поля

Векторное поле 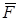называется потенциальным, если оно является градиентом некоторого скалярного поля 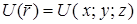, т. е.

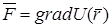, (4.9)

при этом функция 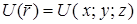называется потенциалом этого векторного поля.

Векторное поле 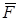потенциально тогда и только тогда, когда 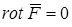, т. е. поле является безвихревым.

Для потенциального поля 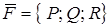с потенциалом 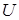выполняются равенства 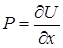, , 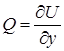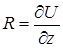и, следовательно, криволинейный интеграл второго рода

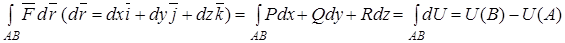(4.10)

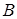не зависит от формы кривой, соединяющей точки и . В случае замкнутого контура интегрирования, когда точки и 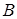совпадают,

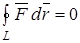, (4.11)

т. е. циркуляция потенциального поля 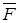по любому замкнутому контуру 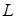равна нулю.

Если поле 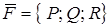является потенциальным, то его потенциал 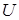может быть найден путем решения системы уравнений с частными производными:

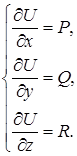(4.12)

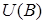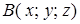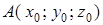Потенциал произвольной точки можно также найти при помощи формулы (4.10) интегрированием по некоторому пути , фиксируя точку . При этом, учитывая независимость этого интеграла от формы пути, путь выбирают в виде ломаной линии, вдоль каждого звена которой изменяется лишь одна координата, а две остальных остаются постоянными.

Пример. Показать, что векторное поле 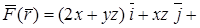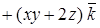потенциально и найти его потенциал.

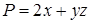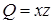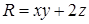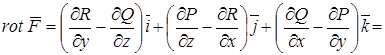
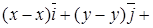
◄ Для данного поля , , . Вычисляем 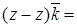= 0. Так как 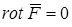, делаем вывод, что поле потенциально. Найдем его потенциал 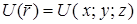при помощи формулы (4.10).

Фиксируя точку 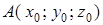, рассмотрим произвольную точку 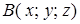. Тогда

.

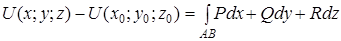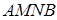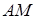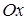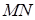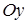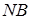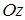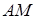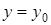Учитывая независимость интеграла от формы пути, линию интегрирования выберем в виде ломаной , где отрезок параллелен оси , отрезок ― оси , а отрезок ― оси . Вдоль имеем и 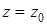, и, следовательно, 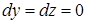; вдоль 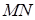переменная 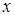постоянна и 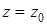, откуда 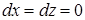; вдоль 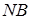две переменные 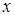и 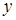постоянны и, следовательно, 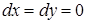. Тогда

.

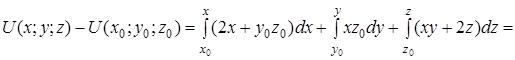
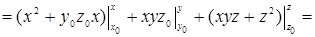
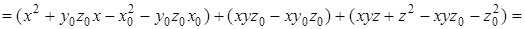
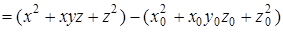Таким образом, . ►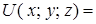

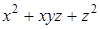Векторное поле 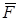называется соленоидальным, если оно является ротором некоторого векторного поля 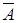, т. е.

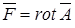. (4.13)

Поле 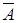называется векторным потенциалом поля .

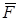Векторное поле 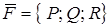соленоидально в том и только в том случае, когда

.

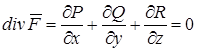Пример. Показать, что векторное поле 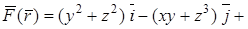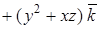соленоидально.

◄ Для данного поля , , 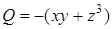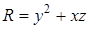. Вычисляем 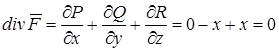. Так как 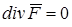, делаем вывод, что поле соленоидально. ►