Векторное поле. Дивергенция и ротор векторного поля
Векторным полем называется область пространства, каждой точке которого отнесен некоторый вектор. Задание векторного поля эквивалентно заданию некоторой векторной функции (вектор-функции)
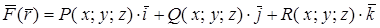 . (4.4)
. (4.4)
Плоским векторным полем называется вектор-функция
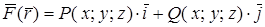 , где
, где 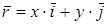 . (4.5)
. (4.5)
Векторными линиями векторного поля 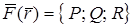 называются линии, касательные к которым в каждой их точке совпадают с направлением векторного поля. Векторные линии поля называют также силовыми линиями или линиями тока.
называются линии, касательные к которым в каждой их точке совпадают с направлением векторного поля. Векторные линии поля называют также силовыми линиями или линиями тока.
Дивергенцией (расходимостью) векторного поля 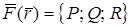 называется скалярное поле, определяемое равенством
называется скалярное поле, определяемое равенством
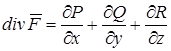 . (4.6)
. (4.6)
Ротором векторного поля 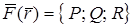 называется векторное поле, определяемое следующим образом:
называется векторное поле, определяемое следующим образом:
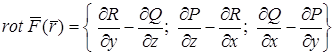 . (4.7)
. (4.7)
Удобной является следующая формальная запись ротора:
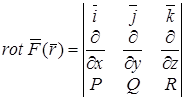 , (4.8)
, (4.8)
где «умножение» символов дифференцирования на одну из функций понимается как взятие соответствующей частной производной этой функции.
Название «ротор» происходит от латинского roto–вращаю. Поводом для такого названия послужило то, что как для твердых, так и для произвольно деформирующихся тел (например, жидкости) 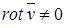 (
( 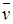 – линейная скорость точки тела) только в тех точках тела, которые находятся во вращательном движении (при этом
– линейная скорость точки тела) только в тех точках тела, которые находятся во вращательном движении (при этом 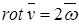 , где
, где 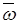 – угловая скорость вращения).
– угловая скорость вращения).
Ротор векторного поля называют иногда вихрем векторного поля.
Пример. Вычислить дивергенцию и ротор векторного поля 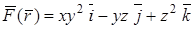 .
.
◄ Дивергенция определяется формулой (4.6). Имеем: 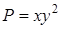 ,
, 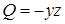 ,
, 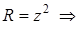
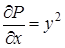 ,
, 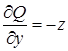 ,
, 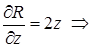
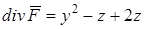 =
= 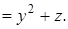
Вычисляем ротор данного векторного поля 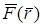 :
:
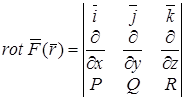 =
= 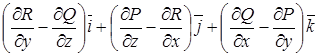 =
= 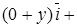
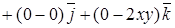 =
= 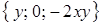 . ►
. ►
Дата добавления: 2016-07-27; просмотров: 10015;











