Призводная по направлению и градиент
Скалярное поле. Производная по направлению и градиент
Скалярное поле
Скалярным полем называется область пространства, каждой точке которого отнесено значение некоторой скалярной величины (величины без направления). Другими словами, скалярное поле – скалярная функция точки в евклидовом пространстве. Так как каждая точка поля может быть определена ее радиусом – вектором 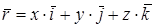 , где
, где 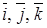 – единичные базисные векторы (рис. 1), задание скалярного поля эквивалентно заданию некоторой скалярной функции
– единичные базисные векторы (рис. 1), задание скалярного поля эквивалентно заданию некоторой скалярной функции 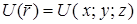 . Скалярное поле в евклидовом пространстве
. Скалярное поле в евклидовом пространстве 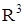 можно рассматривать как обыкновенную функцию
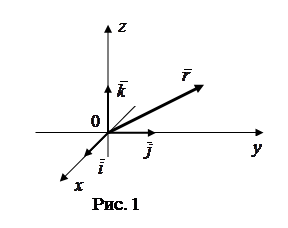
можно рассматривать как обыкновенную функцию 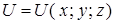 трех переменных. Предполагается, что скалярные функции являются однозначными, непрерывными и дифференцируемыми достаточное число раз.
трех переменных. Предполагается, что скалярные функции являются однозначными, непрерывными и дифференцируемыми достаточное число раз.
 Скалярными полями являются, например, поле температуры неравномерно нагретого тела (
Скалярными полями являются, например, поле температуры неравномерно нагретого тела ( 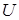 – температура), поле плотности неоднородного тела (
– температура), поле плотности неоднородного тела ( 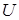 – плотность), поле электростатического потенциала и т. п.
– плотность), поле электростатического потенциала и т. п.
Наряду с определенными выше скалярными полями рассматривают также плоскиескалярные поля, т. е. функции 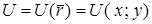 , где
, где 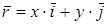 – радиус-вектор произвольной точки плоскости (пространства
– радиус-вектор произвольной точки плоскости (пространства 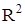 ).
).
Поверхностью уровня скалярного поля 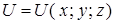 называется множество точек пространства
называется множество точек пространства 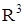 , удовлетворяющих уравнению
, удовлетворяющих уравнению 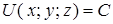 , где
, где 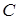 – произвольная постоянная. Поверхности уровня позволяют представить поле геометрически. Аналогично определяется понятие линии уровня плоского скалярного поля
– произвольная постоянная. Поверхности уровня позволяют представить поле геометрически. Аналогично определяется понятие линии уровня плоского скалярного поля 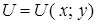 .
.
Понятие поверхности уровня и линии уровня скалярного поля тождественны понятиям, соответственно, поверхности уровня функции 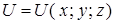 трех переменных и линии уровня функции
трех переменных и линии уровня функции 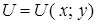 двух переменных.
двух переменных.
Пример. Найти линии уровня плоского скалярного поля 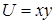 .
.
◄ Приравниваем 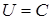 , где
, где 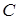 – произвольная постоянная. Отсюда
– произвольная постоянная. Отсюда 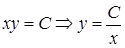 . Кроме того, при
. Кроме того, при 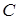 =0 из
=0 из 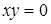 будем иметь
будем иметь 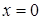 или
или 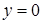 . Таким образом, линиями уровня будут равнобочные гиперболы
. Таким образом, линиями уровня будут равнобочные гиперболы 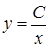 при
при 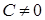 и, кроме того, объединение двух координатных осей, образующих отдельную линию уровня. ►
и, кроме того, объединение двух координатных осей, образующих отдельную линию уровня. ►
Пример. Найти поверхности уровня скалярного поля 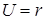 , где
, где 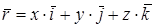 ,
, 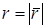 .
.
◄ Приравниваем 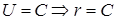 , где
, где 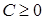 (т. к.
(т. к. 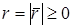 ) – произвольная постоянная. Так как
) – произвольная постоянная. Так как 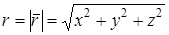 , будем иметь
, будем иметь 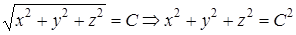 , т. е. поверхностями уровня данного скалярного поля будут концентрические сферы радиуса
, т. е. поверхностями уровня данного скалярного поля будут концентрические сферы радиуса 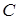 с центром в начале координат.
с центром в начале координат. 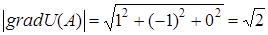
Призводная по направлению и градиент
Градиентом скалярного поля 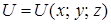 называется вектор (векторное поле, см. ниже)
называется вектор (векторное поле, см. ниже)
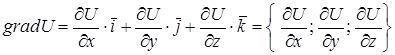 . (4.1)
. (4.1)
Градиент скалярного поля в каждой точке направлен по нормали к поверхностям уровня этого скалярного поля и показывает направление наибольшего роста функции 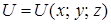 .
.
Величиной градиента называют скалярное поле
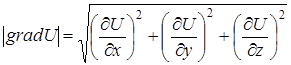 . (4.2)
. (4.2)
Пример. Найти величину градиента скалярного поля 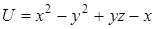 в точке
в точке 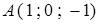 .
.
◄ Находим частные производные функции 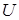 :
: 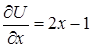 ,
, 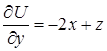 ,
, 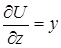 . Таким образом,
. Таким образом, 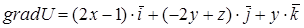 . Подставляя в последнее равенство координаты точки
. Подставляя в последнее равенство координаты точки  , получаем градиент поля в этой точке:
, получаем градиент поля в этой точке: 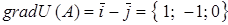 . По формуле (4.2) находим величину градиента данного скалярного поля в точке
. По формуле (4.2) находим величину градиента данного скалярного поля в точке  :
: 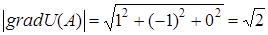 . ►
. ►
Производная по направлению 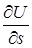 скалярной функции
скалярной функции 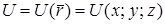 есть скорость изменения функции по отношению к величине перемещения
есть скорость изменения функции по отношению к величине перемещения 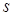 точки вдоль выбранного направления
точки вдоль выбранного направления 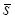 , и может быть найдена по формуле:
, и может быть найдена по формуле:
 . (4.3)
. (4.3)
Из этой формулы видно, что производная функции точки 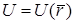 по направлению
по направлению 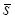 равна проекции вектора градиента
равна проекции вектора градиента 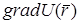 на направление
на направление 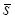 . Отсюда, в частности, следует, что в направлениях, перпендикулярных
. Отсюда, в частности, следует, что в направлениях, перпендикулярных 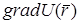 , т. е. касательных к поверхности уровня, производная понаправлению
, т. е. касательных к поверхности уровня, производная понаправлению 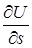 равна нулю.
равна нулю.
Пример. Найти производную скалярного поля 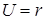 в направлении вектора
в направлении вектора 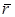 .
.
◄ Так как 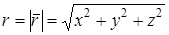 , функция
, функция 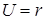 в координатах точки поля будет иметь вид
в координатах точки поля будет иметь вид 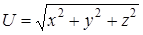 . Находим частные производные данной функции:
. Находим частные производные данной функции: 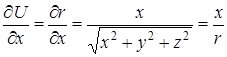 ,
, 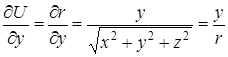 ,
, 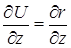 =
= 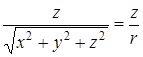 . Следовательно,
. Следовательно, 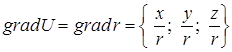 =
= 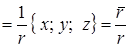 . По формуле (4.3) находим производную данного скалярного поля по направлению
. По формуле (4.3) находим производную данного скалярного поля по направлению 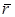 :
: 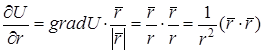 =
= 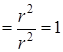 . ►
. ►
Дата добавления: 2016-07-27; просмотров: 3083;











