Циркуляция векторного поля. Формула Стокса

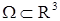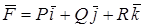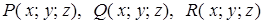Пусть в области задано некоторое векторное поле , где – непрерывно дифференцируемые в области 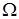функции. Пусть 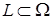– гладкая кривая, расположенная в области 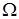, на которой выбрано одно из двух возможных направлений (считающееся положительным направлением).

Криволинейный интеграл

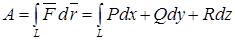(4.20)

называется работой векторного поля вдоль кривой 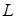. Если 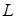– замкнутая кривая, то интеграл

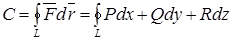(4.21)

называется циркуляцией векторного поля 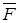вдоль кривой .

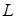Если 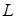– замкнутая гладкая кривая (контур), являющаяся границей поверхности 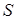, то имеет место формула Стокса:

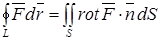(4.22)

(циркуляция векторного поля 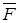по замкнутой кривой 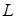равна потоку ротора этого поля через поверхность 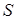, опирающуюся на кривую 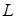), причем направление обхода контура 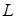выбрано так, что при взгляде с конца вектора 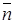оно происходит против часовой стрелки (направление обхода контура и направление нормали образуют правовинтовую систему).

В случае плоского векторного поля 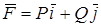формула стокса переходит в формулу Грина:

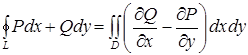. (4.23)

В формуле (4.22) поверхность 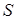может быть любой формы, т. е. через любые две поверхност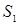и и 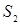, если только они опираются на один и тот же контур 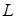, проходит одинаковый поток ротора любого непрерывного вектора 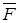, равный циркуляции этого вектора по общему контуру этих поверхностей.

Из (4.22) следует, в частности, что

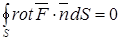, (4.24)

так как в случае замкнутой поверхности 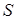контур 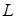стягивается в точку и, следовательно, циркуляция по нему равна нулю.

Пример. Найти работу плоского векторного поля 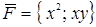вдоль кривой 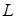, являющейся частью параболы 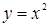, от точки 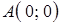до точки .

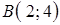◄ Так как 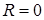(поле плоское) и вдоль кривой 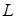переменные связаны равенством 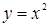(отсюда 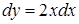), согласно формуле (4.20) будем иметь: . ►

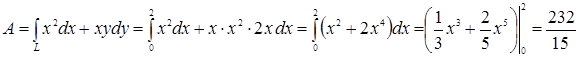Пример. Вычислить циркуляцию плоского векторного поля 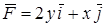по контуру 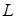треугольника 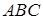с вершинами 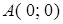, , 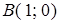, 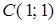обходя его в положительном направлении (против часовой стрелки).

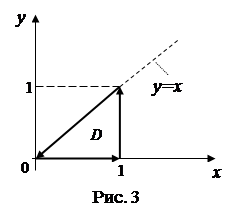◄ Вычислим искомую циркуляцию при помощи формулы Грина (4.23), где областью 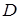является треугольник 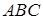(рис. 3). Так как для заданного поля 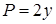, 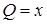и, следовательно, 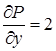, а 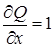, для его циркуляции вдоль 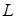будем иметь: = = . ►

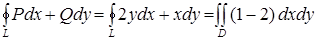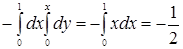Лекция №13

Тема 23. Основные понятия теории вероятностей.