Показатели размера и интенсивности вариации
Показатели вариации делятся на 2 группы: абсолютные и относительные. К абсолютным показателям относятся:размах колебаний (R), среднее линейное отклонение , дисперсия, среднее квадратическое (стандартное) отклонение.К относительным показателям вариацииотносятся: коэффициент вариации, относительное линейное отклонение и др..
 Размах колебаний, или размах вариации представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: . Размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями.Так как только два значения признака учитываются, причем крайние, размах вариации может быть зависимым от случайных причин.
Размах колебаний, или размах вариации представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: . Размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями.Так как только два значения признака учитываются, причем крайние, размах вариации может быть зависимым от случайных причин.
 Среднее линейное отклонение ( ) –сумма всех отклонений, условно принятых содинаковым знаком (по модулю), разделенная на их число.Среднее линейное отклонение более полно характеризует колеблемость признака.
Среднее линейное отклонение ( ) –сумма всех отклонений, условно принятых содинаковым знаком (по модулю), разделенная на их число.Среднее линейное отклонение более полно характеризует колеблемость признака.
Дисперсия  (σ2) -средняя из квадратов отклонений вариантов значений признака от их средней величины .
(σ2) -средняя из квадратов отклонений вариантов значений признака от их средней величины .
Среднее квадратическое отклонение(  σ)- квадратный корень из дисперсии. Среднее квадратическое отклонение также, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняется конкретное значение признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется соотношение
σ)- квадратный корень из дисперсии. Среднее квадратическое отклонение также, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняется конкретное значение признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется соотношение 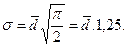
 Зная это соотношение, можно по известному показателюопределить неизвестный, например, по определить σ и наоборот. Среднее квадратическое отклонение измеряет абсолютный размер колеблемости и выражается в тех же единицах измерения, что и значения признака (в рублях, тоннах, процентах и т.д.). Оно является абсолютной мерой вариации.
Зная это соотношение, можно по известному показателюопределить неизвестный, например, по определить σ и наоборот. Среднее квадратическое отклонение измеряет абсолютный размер колеблемости и выражается в тех же единицах измерения, что и значения признака (в рублях, тоннах, процентах и т.д.). Оно является абсолютной мерой вариации.
Формулы расчета показателей вариации для несгруппированных и сгруппированных данных приведены в табл.1.9.
Таблица 1.9
Методика расчета показателей вариации
| Показатель | Формулы расчета показателей | |
| для несгруппированных данных | для сгруппированных данных | |
| Среднее линейное отклонение | 
| 
|
| Дисперсия | 
| 
|
| Среднее квадратическое отклонение | 
| 
|
Для оценки интенсивности вариации, а также для сравнения ее величины в разных совокупностях или по разным признакам используют относительные показатели вариации (коэффициент осцилляции, коэффициент вариации и др.), которые рассчитываются как отношение абсолютных показателей к средней величине признака. Коэффициент осцилляции (относительный размах вариации) есть отношение размаха вариации R к средней арифметической 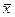 .
.
По своему абсолютному значению среднее квадратическое отклонение зависит не только от степени вариации признака, но и от абсолютных уровней вариант и средней. Чтобы сравнивать, нужно найти удельный вес отклонения в среднем арифметическом показателе, выраженный в % , то есть рассчитать относительные показатели вариации.
Линейный коэффициент вариации это отношение среднего линейного отклонения к средней арифметической, выраженный в %.

Коэффициент вариации , как отношение среднего квадратического отклонения к среднему арифметическому, - измеряет колеблемость в относительном выражении, относительно среднего уровня .

Также этот показатель используют для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. Существует шкала степени однородности совокупности в зависимости от значений коэффициента вариации.
| Коэффициент вариации (%) | Степень однородности совокупности |
| До 30 | Однородная |
| 30-60 | Средняя |
| 60 и более | Неоднородная |
Средние величины и показатели вариации могут быть рассчитаны через моменты распределения. Моментом k-го порядка называют среднюю из k-х степеней отклонений вариантов x от некоторой постоянной величины А. ЕслиА= 0, момент называется начальным. Если А= 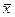 , момент называется центральным. Если А ≠ 0, момент называют условным, а расчет средних с его использованием называется методом условных моментов. Согласно определению начальный момент первого порядка есть средняя арифметическая, а момент второго порядка – есть дисперсия.
, момент называется центральным. Если А ≠ 0, момент называют условным, а расчет средних с его использованием называется методом условных моментов. Согласно определению начальный момент первого порядка есть средняя арифметическая, а момент второго порядка – есть дисперсия.
Расчет средней и дисперсии методом условных моментов производится по формулам:
Условный момент первого порядка
 |  |
Условный момент второго порядка
 |  |
где m1, m2 – условные моменты первого и второго порядка,
к – общий множитель.
Также как средняя арифметическая, дисперсия обладает рядом важных свойств, которые используют в статистическом анализе:
1) дисперсия постоянной величины равна нулю;
2)если все варианты значений признака уменьшить на одно и то же число A, то дисперсия не изменится;
3)если все варианты значений признака уменьшить в одно и то же число раз (k раз), то дисперсия уменьшится в k2 раз;
4)дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной:

Дата добавления: 2020-10-25; просмотров: 1306;











