Мода и медиана, их смысл и значение
Важным видом средних величин являются структурные (непараметрические) средние. Их используют для изучения внутреннего строения и структуры рядов распределения значений признака. К основным видам структурных средних относят моду и медиану.
Мода это величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном дискретном ряду модой выступает варианта, имеющая наибольшую частоту.
Медиана это варианта, которая находится в середине ранжированного вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности. В ранжированных рядах несгруппированных данных медиана равна значению признака, расположенного строго в середине ряда. В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда. Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:

Рассмотрим определение моды и медианы по несгруппированным данным. Предположим, что 9 торговых фирм города реализуют товар А по следующим оптовым ценам (тыс. руб.):
4,4;4,3;4,5;4,5;4,3; 4,3;4,6; 4,2; 4,6.
Чаще всего встречается цена 4,3 тыс. руб., эта величина и будет модой.
Для определения медианы необходимо провести ранжирование:
4,2; 4,3; 4,3; 4,3;4,4;4,5;4,5; 4,6; 4,6
Центральной в этом ряду является цена 4,4 тыс. руб., эта величина и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.
Например, чтобы дать характеристику среднего дохода группы людей, насчитывающей 10 человек, из которых 9 человек имеют доход от 100 до 500 долл. в месяц, а месячные доходы последнего составляют 50000 долл. (табл. 1.7-1), лучше всего рассчитать медиану. Она составит 310 долл., как средняя между 5-ым и 6-ым работником.
Медиана (как и мода ) в отличие от средней арифметической не зависит от минимального и максимального значений ряда распределения и потому практически выполняет функции средней для неоднородной совокупности и в случаях, когда между минимальным и максимальным значениями изучаемого признака имеют место резкие различия (как в приведенном примере).
Таблица 1.7-1
| № п/п | ||||||||||
| Доход (долл.) |
Моду и медиану можно рассматривать как порядковые характеристики значения признака у единицы совокупности, занимающей особое место в ряду распределения. Мода является величиной, вокруг которой группируется наибольшее количество единиц совокупности. Медиана отражает значение признака, сумма отклонений от которого является наиментшей величиной. Средняя арифметическая часто используется как показатель центра распределения, положительные и отрицательные отклонения от которого индивидуальных значений признака взаимно погашаются. При нормальном распределении все эти средние показатели одинаковую величину.
Вдискретном вариационном ряду определение медианного значения признака сводится к определению номера медианной единицы ряда по формуле

где n — объем совокупности.
Полученное значение показывает, где точно находится номер медианной единицы (номер середины ряда). Медианное значение характеризуется тем, что его кумулятивная частота (сумма накопленных частот по группам) равна половине суммы всех частот или превышает ее.
Рассмотрим пример расчета моды и медианы по сгруппированным данным в дискретном вариационном ряду. Исходные данные приведены в табл. 1.7-2.
Для определения медианы находят номер медианной единицы ряда по формуле:
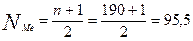
Точная середина находится между 95 и 96 предприятиями упорядоченной совокупности. Необходимо определить в какой группе находятся предприятия с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты.Как видноиз таблицы 1.7-2, эти предприятия находятся в третьей группе, в которой товары продали по цене 54 руб за ед.. Следовательно, медиана равна 54 руб за ед. .
А вот мода будет в следующей группе (55 руб. за ед.), так как наибольшая частота (f=60) приходится на эту группу. Модальный интервал в интервальном ряду определяется по наибольшей частоте.
Таблица1.7-2
Определение моды и медианы дискретного вариационного ряда
| Цена, руб. за единицу Х | Число торговых предприятий, f | Накопленные частоты, F |
| 60=12+48 | ||
| 116=60+56 | ||
| 176=116+60 | ||
| 190=176+14 | ||
| Всего |
Для определения медианного интервала необходимо рассчитать суммы накопленных частот. Медианный интервал характерен тем, что его кумулятивная частота равна полусумме всех частот ряда или превышает ее.
Методика расчета моды и медианы в интервальных рядах с равными интервалами приведена в табл.1.8.
Соотношение моды , медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Таблица 1.8
Методика расчета показателя моды и медианы в интервальных рядах с равными интервалами
| Вид средней | Методика расчета показателя |
| Мода | мода вычисляется по формуле:
 где — минимальная граница модального интервала;
где — минимальная граница модального интервала;
 — величина модального интервала; — величина модального интервала;
 — частота модального интервала; — частота модального интервала;
 — частота интервала, предшествующего модальному интервалу; — частота интервала, предшествующего модальному интервалу;
 — частота интервала, следующего за модальным. — частота интервала, следующего за модальным.
|
| Медиана | В интервальном ряду с равными интервалами медиана рассчитывается по формуле
 где — начальное значение медианного интервала;
где — начальное значение медианного интервала;
  — величина медианного интервала;
— сумма частот ряда; — величина медианного интервала;
— сумма частот ряда;
  — сумма накопленных частот в интервалах, предшествующих медианному;
— частота медианного интервала. — сумма накопленных частот в интервалах, предшествующих медианному;
— частота медианного интервала.
|
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1.Какова роль статистических показателей в управлении экономикой?
2.Какие могут быть выделены группы обобщающих статистических показателей?
3.Назовите виды относительных величин и охарактеризуйте их значение.
4.Для чего рассчитывают относительные величины координации?
5.Почему важно анализировать абсолютные и относительные показатели во взаимосвязи?
6.Что представляет собой средняя величина и в чем состоит ее определяющее свойство?
7.Напишите формулу средней арифметической и приведите пример исчисления средней по формуле:
а) средней арифметической простой;
б) средней арифметической взвешенной.
8.Какова роль средних величин в обобщении данных статистического наблюдения?
9.Для каких целей используется формула средней геометрической?
10.Назовите основные свойства средней арифметической .
11.В чем различие между степенными и структурными средними?
12. Использование моды и медианы и их расчет по несгруппированным данным.
ТЕСТЫ
1. Укажите относительные величины структуры. В текущем году:
а) на строительство объектов социально-культурной сферы было направлено 17 % всех инвестиций области;
б) коммунальные услуги подорожали на 75 % по сравнению с предшествующим годом.
3. Укажите относительные величины динамики:
а) производство электроэнергии в стране увеличилось в отчетном периоде по сравнению с базисным на 200 млрд. кВт-ч.;
Дата добавления: 2020-10-25; просмотров: 1229;











