Дисперсионный анализ
Наряду с изучением вариации по всей совокупности в целом можно изучить количественные изменения по группам, на которые разделяется совокупность, и между группами. Для этого выделяют три вида дисперсии: общую, межгрупповую и внутригрупповую.
Общая дисперсия(дисперсия признака по всей изучаемой совокупности) характеризует вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности и может быть рассчитана по формуле:

 Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризуетмежгрупповая дисперсия , которая является мерой колеблемости групповых средних вокруг общей средней и исчисляется по формуле:
Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризуетмежгрупповая дисперсия , которая является мерой колеблемости групповых средних вокруг общей средней и исчисляется по формуле:
где m - число групп;
 - число единиц в группе ;
- число единиц в группе ;

- частная средняя по группе;

- общая средняя по всей совокупности единиц.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группегрупповая (внутригрупповая) дисперсия:

По совокупности в целом вариация значений признака под влиянием прочихфакторов характеризуется средней из групповых дисперсий:

 Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий
Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий
Данное соотношение называется правилом сложения дисперсий и используется в ряде методов статистики, в частности при расчете ошибок выборочного наблюдения (Тема 1.1) и при измерении тесноты связи между признаками (тема 2.1). Теоретический и практический интерес к этому правилу заключается , во-первых, в том что, зная две величины, на основе приведенного равенства всегда можно определить третью величину, во-вторых, важное значение состоит в том что, зная общую дисперсию и дисперсию групповых средних, можно оценить силу влияния группировочного признака с помощью эмпирического коэффициента детерминации и эмпирического корреляционного отношения.
Эмпирический коэффициент детерминации равен отношению межгрупповой и общей дисперсии и рассчитывается по формуле:

Он показывает, какая часть (доля) общей вариации изучаемого признака обусловлена вариацией группировочного признака.
Эмпирическое корреляционное отношение (ή) представляет собой корень квадратный из эмпирического коэффициента детерминации и рассчитывается следующим образом:

Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака (изменяется в пределах от 0 до 1. Если ή = 0, то признак не оказывает влияния на результативный. Если ή = 1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Что такое размах вариации и в чем его особенности как показателя вариации?
2. Назовите показатели, являющиеся абсолютными характеристиками степени вариации.
3. Что такое размах вариации и в чем его особенности как показателя вариации?
4. Назовите показатели, являющиеся абсолютными характеристиками степени вариации.
5. В чем состоят особенности расчета показателей вариации по сгруппированным данным?
6. Какое аналитическое значение имеет коэффициент вариации?
7. Что представляет собой дисперсия альтернативного признака?
8. Назовите показатели, относящиеся к квантилям распределения.
9. Как определяется внутригрупповая дисперсия?
10. Что представляет собой правило сложения дисперсий?
11. Что характеризует межгрупповая дисперсия, формула ее расчета?
12. Что называется эмпирическим корреляционным отношением, и как оно интерпретируется?
13. В чем состоит значение проверки гипотезы о форме распределения?
14. Каковы особенности кривых нормального распределения? Их использование в анализе фактических данных.
15. Какие критерии согласия используются наиболее часто?
ТЕСТЫ
1. Средняя себестоимость выпускаемой продукции в двух группах предприятий одинаковая. В первой группе предприятий индивидуальные уровни себестоимости составляют: 23; 52; 30; 28; 37. Во второй группе: 30; 55; 20; 46; 19. Вариация себестоимости больше:
1) в первой группе предприятий;
2) во второй группе предприятий;
3) одинакова;
4) сравнить вариации себестоимости нельзя.
2. Среднее значение признака в двух совокупностях одинаково. Может ли быть различной вариация признака в этих совокупностях?
а) да;б) нет.
3. Средние значения признака в двух совокупностях неодинаковы. Может ли быть одинаковой вариация признака в этих совокупностях?
в) да; г) нет.
4. Средняя выработка токарей в двух бригадах по 28 деталей за смену. В первой бригаде индивидуальная выработка рабочих составляет: 32; 25; 29; 28; 26. Во второй бригаде: 30; 25; 22; 36; 27. Вариация сменной выработки больше:
1) в первой бригаде;
2) во второй бригаде;
3) одинакова;
4) сравнить вариации сменной выработки нельзя.
5. Средний суточный объем производства продукции на двух промышленных предприятиях района за отчетный месяц одинаковый - по 140 млн. д. ед. По декадам месяца он распределяется следующим образом:
| Декады | |||
| Предприятие № 1 | |||
| Предприятие № 2 |
Укажите, пользуясь показателями вариации, какое из предприятий работало более ритмично:
1) предприятие № 1;
2) предприятие № 2;
3) ритмичность работы на обоих предприятиях одинакова;
4) сравнить ритмичность работы предприятий нельзя.
6. Какая из приведенных формул используется для расчета среднего квадратического отклонения?
1) 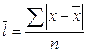 ;
;
2) 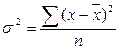 ;
;
3) 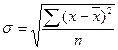 ;
;
4) 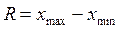 .
.
7. Какая из приведенных формул используется для расчета дисперсии?
1) 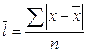 ;
;
2) 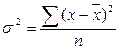 ;
;
3) 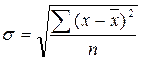 ;
;
4) 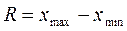 .
.
8. Какая из приведенных формул используется для расчета размаха вариации?
1) 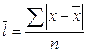 ;
;
2) 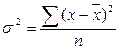 ;
;
3) 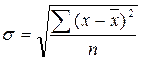 ;
;
4) 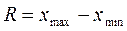 .
.
9. Какая из приведенных формул используется для расчета среднего линейного отклонения?
1) 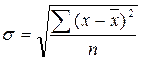 ;
;
2) 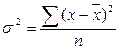 ;
;
3) 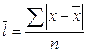 ; 4)
; 4)
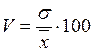 .
.
10. Вариацию признака, обусловленную влиянием признака-фактора, положенного в основу группировки, характеризует:
1) межгрупповая дисперсия;
2) частная (внутригрупповая) дисперсия;
3) средняя из частных (внутригрупповых) дисперсий;
4) общая дисперсия.
11. Вариацию признака под влиянием прочих факторов (помимо признака-фактора, положенного в основу группировки), действующих в совокупности, характеризует:
1) межгрупповая дисперсия;
2) частная (внутригрупповая) дисперсия;
3) средняя из частных (внутригрупповых) дисперсий;
4) общая дисперсия.
12. Вариацию признака, обусловленную влиянием всех факторов, действующих в совокупности, характеризует:
1) межгрупповая дисперсия;
2) частная (внутригрупповая) дисперсия;
3) средняя из частных (внутригрупповых) дисперсий;
Общая дисперсия.
13. Вариацию признака только за счёт условий и причин, действующих внутри одной из групп, выделенных в составе совокупности, отражает:
1) межгрупповая дисперсия;
2) частная (внутригрупповая) дисперсия;
3) средняя из частных (внутригрупповых) дисперсий;
4) общая дисперсия.
14. Для определения эмпирического корреляционного отношения, которое характеризует тесноту связи между результативным и факторным признаком, используется формула:
1) 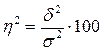 ;
;
2) 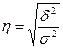 ;
;
3) 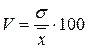 ;
;
4) 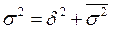 .
.
15. Закон (правило) сложения дисперсий выражается следующей формулой:
1) 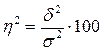 ;
;
2) 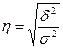 ;
;
3) 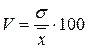 ;
;
4) 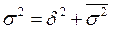 .
.
16. Для определения коэффициента вариации, который характеризует однородность совокупности и типичность средней величины, используется формула:
1) 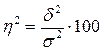 ;
;
2) 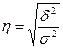 ;
;
3) 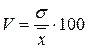 ;
;
4) 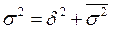 .
.
17. Для определения коэффициента детерминации, который характеризует долю вариации результативного признака, обусловленную признаком-фактором, положенным в основу группировки, в общей вариации признака, используется формула:
1) 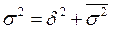 ;
;
2) 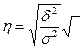 ;
;
3) 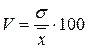 ;
;
4) 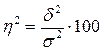 .
.
Открытого типа
18. По данным ряда распределения студентов по уровню успеваемости определите средний уровень успеваемости в группе (округлить до 0,1).
| Экзаменационный балл | |||||
| Число студентов, чел. |
(2*3 +3*7 + 4*13 +5*7 )/5 =3.8 (4)
19. По данным задания 108 определите медиану и первый квартиль экзаменационного балла.
Ме =4, кВ= 3
20. По данным задания 108 определите среднее линейное отклонение экзаменационного балла студентов в группе от среднего.
Д = (2*3 + 1*7 +1*7) :30 =0.67
21. По данным ряда распределения рабочих по уровню заработной платы определите средний уровень зарплаты рабочих цеха (округлить до 0,1).
| Заработная плата, тыс. руб. | 3,5 | 4,0 | 4,5 | 5,0 | 2,5 | 6,0 |
| Число рабочих, чел. |
(3.5 +4*3 +4.5*6 +5*10+ 2.5*2 +6*2):24 =4.5625(4.6)
22. По данным задания 110 определите моду и второй квартиль заработной платы.
Мо = 5 Q2= 4.5
23. По данным задания 110 определите среднее квадратическое отклонение заработной платы рабочих цеха от среднего ее уровня.
(1.1*1.1+3*0.6*0.6 +6*0.1*0.1 + 10*0.4*0.4 +2.1*2.1*2+1.4*1.4* 2) =1.21+1.08+0.06+1.6+8.82+3.92 =16.69
√16.69/24 =√0.69 =0.83
24. По данным ряда распределения рабочих по уровню квалификации (по тарифному разряду) определите средний уровень квалификации рабочих предприятия (округлить до 0,1).
| Тарифный разряд | ||||||
| Число рабочих, чел. |
(2+2*3 +3*25+4*70 +5*10+6*5): 115=443:115 =3.85 (3.8)
25. По данным задания 112 определите медиану и первый дециль тарифного разряда.
Ме= 4 Д= 3
Раздел 2.1
Дата добавления: 2020-10-25; просмотров: 798;











