Понятие о вариации и задачи ее изучения

Статистический анализ вариации предполагает выполнение следующих основных этапов [6, с.50]:

1. Построение вариационного ряда.

2. Графическое изображение вариационного ряда.

3. Расчет показателей центра распределения и структурных характеристик вариационного ряда.

4. Расчет показателей размера и интенсивности вариации.

5. Оценка вариационного ряда на асимметрию и экцесс.

Для характеристики среднего значения признака в вариационном ряду используются так называемые показатели центра распределения, к которым относятся средняя арифметическая, мода и медиана ( Тема 1.3, c.). Моду и медиану можно определить и графически.

Моду можно определить по гистограмме или кривой распределения. Для определения по гистограмме нужно взять столбец, имеющий наибольшую высоту,и из его левого верхнего угла провести отрезок в верхний угол последующего столбца, а из правого угла- в верхний правый угол предыдущего.. Абцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности. Абцисса наивысшей точки кривой распределения, соответствующая наибольшей частоте, будет также соответствовать модальному значению признаку совокупности.

Медиану приближенно определить по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абцисс, до пересечения ее с кумулятой.Абцисса точки епресечения и является медианой.

Расчет модального и медианного значений для вариационных рядов с неравными интервалами осуществляется по формулам, аналогичным приведенным выше (тема 1.3 с. ), только вместо показателей частот (частостей) используются абсолютной или лтносительнойплотности распределения, которые обеспечивают сопоставимость неравных интервалов. Показатели плотности распределения находятся как отнощение частот (частостей) к величине интервала h:

- абсолютная плотность распределения f¹

f ¹= f / h;

- относительная плотность распределения w¹

w¹ = w / h.

По соотношению характеристик центра распределения можно судить о симметричности эмпирического ряда распределения. Симметричным является распределение , в котором частоты двух вариантов, равноотстоящих в обе стороныот центра распределения, равны между собой. В симметричном (нормальном) ряду распределения средняя величина 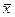, медиана Ме и мода Мо равны между собой:

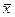= Ме = Мо.

Если 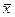< Ме < Мо, то имеет место левосторонняя асимметрия, при которой большая часть единиц совокупности имеет значение признака ниже модального. На графике распределения левая ветвь относительно максимальной ординаты вытянута меньше, чем правая.

Если 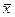> Ме > Мо, то имееи место правосторонняя асимметрия, при которой большая часть единиц совокупности имеет значение признака больше модального. На графике распределения правая ветвь вытянута больше, чем левая.

Для оценки степени асимметричности применяют моментный и структурный коэффициенты асимметрии.

Моментный коэффициент асимметрии As (стандартизованный момент третьего порядка) определяется по формуле:

As = M₃ / σ³,

где M₃ – центральный момент третьего порядка,

где М₃= .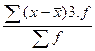

Структурный коэффициент асимметрииПирсона определяется по формуле: Аs = 3( 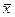- Ме)/ σ.

На направление асимметрии указывает знак коэффициента: если Аs < 0, то это левосторонняя асимметрия (ее называют таже отрицательной), при правосторонней асимметрии Аs >0.

Другим свойством рядов распределения является экцесс. Под экцессом понимают островершинность или плосковершинность распределения по сравнению с нормальным. Экцесс оценивают с помощью центрального момента четвертого порядка М₄ по формуле:

Es = М₄ / σ⁴