Принципы теории вероятностей.

Принцип сложения.

Напомним, что два события называются несовместными, если они одновременно произойти не могут, то есть, если АВ=Ø и совместными в противном случае. Следующие четыре утверждения и образуют принцип сложения.

Теорема 1. Для любого события 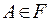имеет место следующее равенство: .

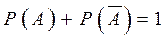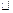. Действительно, так как 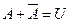, то .

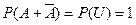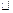
Теорема 2. Если 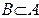, то Р(А-В)=Р(А)–Р(В).

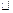Имеем очевидное равенство А=В+(А-В), где В и А-В являются несовместными событиями. Используя аксиому 3 вероятности, имеем Р(А-В)=Р(А)–Р(В).

Теорема 3. (теорема сложения вероятностей). Пусть мы имеем два совместных события А и В. Тогда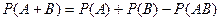

Преобразуем их сумму в сумму несовместных событий

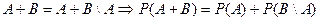
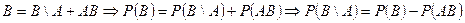
Подставляя второе выражение в первое, получим

.

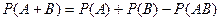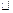
Пример. По мишени один раз стреляют два стрелка. Вероятность попадания первого стрелка в мишень р₁ = 0,7, второго – р₂ = 0,8. Какова вероятность того, что кто-нибудь из них попадет в мишень?

А = А₁ + А₂, А попадание в мишень; А₁ – попал первый стрелок; А₂ – попал второй стрелок.

Р(А) =Р(А₁ + А₂)=Р(А₁)+ Р(А₂) –Р(А₁А₂)= Р(А₁)+Р(А₂) – Р(А₁ )Р(А₂)= 0.7+ 0,8 – 0,7· 0,8 = 0,94.

Получим вероятность суммы трех совместных событий.

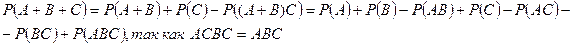
Получена формула

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС)

Обобщая полученный результат на сумму n совместных событий, получим формулу

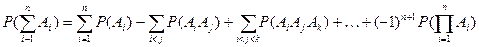
Теорема 4. Для произвольных случайных событий А1, А2, …, Аn 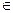F имеет место равенство

.

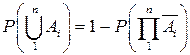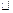. Учитывая, что события 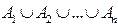и 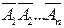являются взаимно противоположными, из теоремы 1 сразу получаем искомое равенство.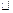

Принцип умножения.

Определение 1. Вероятность события А при условии, что событие В наступило, называется условной и обозначается Р(А/В). Если никаких дополнительных условий не накладывается, то вероятность называется безусловной. Это – обычная, определенная выше вероятность.

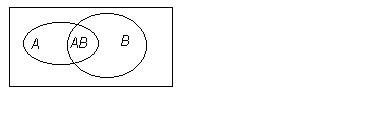
Пример. Пусть в аудитории присутствует N студентов. Среди них N_A – число студентов, регулярно прогуливающих математику, N_B – прогуливающих всё остальное, N_АВ – прогуливающих и математику, и всё остальное. Выбираем одного студента. Введем следующие события:

Пустьсобытие А – случайно выбранный студент, прогуливающий математику, событие В – прогуливающий всё остальное, событие АВ – прогуливающий и математику, и всё остальное. На диаграммах Венна это выглядит так.

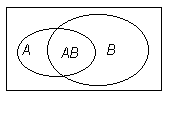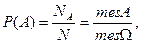
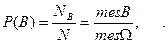
Тогда вероятности этих событий равны: 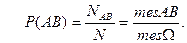Это безусловные вероятности.

Предположим теперь, что мы захотели узнать вероятность того, что случайно выбранный прогульщик всего остального, прогуливает еще и математику. В этом случае количество всех возможных исходов N_B (выбираем только прогульщиков всего), а количество благоприятных исходов – N_АВ. Получим

= =

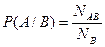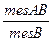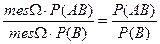
В общем случае имеет место

Определение 2. Условная вероятность события А при условии, что событие В произошло, определяется с помощью следующего равенства:

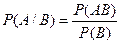, Р(В)>0. Аналогично определяется условная вероятность события В при условии, что событие А произошло: 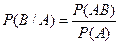, Р(А)>0

Следующее утверждение называют принципом умножения.

Теорема 1. Для любых случайных событий А,ВÎF имеет место следующее равенство:

Р(АВ)=Р(B)Р(А/В) или Р(АВ)=Р(А)Р(В/А).

В случае независимых случайных событий Р(А/В)=Р(А) и Р(В/А)=Р(В); поэтому теорему умножения для независимых случайных событий можно переписать в виде Р(АВ)=Р(А)Р(В). Это равенство используют в качестве определения независимых случайных событий. Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий.

.

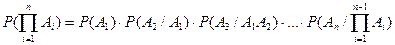Событие А будем называть независимым от события В, если P(A/B) = P(A), т.е. если условная вероятность равна безусловной.

Определение 3. Два события называются независимыми, если наступление одного из них не изменяет вероятность другого. В противном случае события называются зависимыми.

Определение 4. События А₁, А₂,…, А_n называются независимыми в совокупности, если вероятность их произведения равна произведению их вероятностей

.

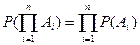Пример. Два стрелка, независимо друг от друга стреляют по одной мишени, произведя залп. Вероятности попадания в мишень для первого стрелка 0,9; для второго – 0,8. Найти вероятность того, что и мишени будет а) одна дырка; б) две дырки; в) хоть одна дырка;

Пусть А – попадание в мишень первого стрелка; В – попадание в мишень второго стрелка. Тогда 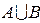– поражение мишени (хотя бы одним стрелком), 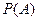- поражение мишени первым стрелком, 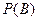- поражение мишени вторым стрелком. а) 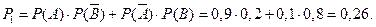б) 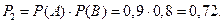в) Имеем 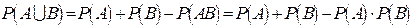, то есть 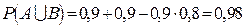.Или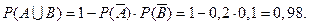

Определение 2. Назовем событие А, событие В и событие С независимыми в совокупности, если выполняются условия:

р(АВ)=р(А)р(В), р(АС)=р(А)р(С), р(ВС)=р(В)р(С), Р(АВС)=р(А)р(В)р(С).

Аналогично определяется понятие независимости в совокупности и большего числа событий. Из определения независимости событий в совокупности следует, что формула умножения вероятностей для независимых в совокупности событий имеет вид

.

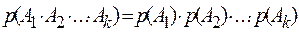Очевидно, что из независимости в совокупности следует попарная независимость случайных событий, однако можно показать, что из попарной независимости не вытекает независимость в совокупности.

Задача Бернштейна.Бросанем правильный тетраэдр, 3 грани которого окрашены соответственно в синий, красный, зеленый цвета, четвертая же грань окрашена всеми этими цветами одновременно. Если С, К, З – случайные события, заключающиеся в том, что тетраэдр падает на грани, окрашенные соответственно в синий, красный и зеленый цвета, то эти события попарно независимы, но не являются независимыми в совокупности.

Действительно, Р(СК)=1/4=0,5∙0,5=Р(С)×Р(К); следовательно, события С и К независимы. Аналогично Р(СЗ)=Р(С)×Р(З) и Р(КЗ)=Р(К)×Р(З). Таким образом, случайные события С,К,З – попарно независимы. Но Р(СКЗ)=1/4≠1/8=P(С)P(К)P(З); следовательно, они не являются независимыми в совокупности.