Полная вероятность и формула Байеса
Решим задачу о Тезее, который, выбираясь из лабиринта, в пункте А потерял нить Ариадны. Какова вероятность того, что он придет в пункт В? Тезей случайным образом выходит на ту или иную дорогу, то есть событие В происходит с одним и только с одним из полной группы попарно несовместных событий 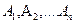 . Они называются гипотезами. Известны вероятности этих событий
. Они называются гипотезами. Известны вероятности этих событий 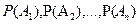 . Но далее из каждого пункта он попадет в пункт В с различной вероятностью. Эти вероятности обозначим
. Но далее из каждого пункта он попадет в пункт В с различной вероятностью. Эти вероятности обозначим 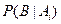 , где i принимает значения от 1 до n. Требуется вычислить полную вероятность Р(В) того, что Тезей попадет из пyнкта А в пункт В. Другими словами, пусть требуется определить вероятность события В, которое может произойти в сочетании с одним из событий А1, А2,…, Аn, образующих полную группу несовместных событий (
, где i принимает значения от 1 до n. Требуется вычислить полную вероятность Р(В) того, что Тезей попадет из пyнкта А в пункт В. Другими словами, пусть требуется определить вероятность события В, которое может произойти в сочетании с одним из событий А1, А2,…, Аn, образующих полную группу несовместных событий ( 
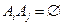 ,
, 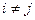 ). Эти события будем называть гипотезами.
). Эти события будем называть гипотезами.
 |  | ||

А1 А2 А3


ВА1 ВА2 ВА3
ВАn-2 ВАn-1 ВАn
Аn-2 Аn-1 Аn
Применяя формулу для вероятности суммы несовместных событий, получимформулу полной вероятности.: 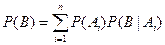 . Вероятности
. Вероятности 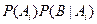 называются априорными( a priori – (лат.) до того).
называются априорными( a priori – (лат.) до того).
Теорема гипотез Байеса. Пусть теперь известно, что событие В произошло. Тогда  .
.
Требуется найти вероятности 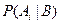 i=l, 2, ..., n - вероятности гипотез после опыта. Они называются апостериорными( a posteriori – (лат.) после того). Используя теорему умножения вероятностей, имеем P(ВАi) =
i=l, 2, ..., n - вероятности гипотез после опыта. Они называются апостериорными( a posteriori – (лат.) после того). Используя теорему умножения вероятностей, имеем P(ВАi) = 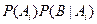 =
= 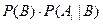
Из последнего равенства получим формулу Байеса  , i=1, 2, …, n, где Р(В) есть полная вероятность осуществления события В.
, i=1, 2, …, n, где Р(В) есть полная вероятность осуществления события В.
Пример. Имеются 2 урны, в каждой из которых находится по 10 шаров, причем в 1-й урне 7 белых и 3 черных шара, во 2-й – 2 белых и 8 черных. наудачу из одной из урн вынимается шар. а) Найти вероятность того, что вынут белый шар. б) шар оказался белым. Найти вероятность того, что он вытянут из второй урны.
а) Пусть В – вытягивание белого шара. А1 –выбор первой урны, А2 – выбор второй урны, Тогда Р(В) можно вычислить по формуле полной вероятности 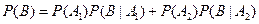 , то есть
, то есть 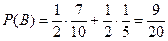 . б) . По формуле Байеса имеем
. б) . По формуле Байеса имеем 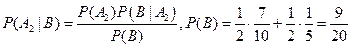 , тогда
, тогда 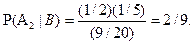
Пример. Мышка наугад выбирает одну из двух одинаковых кормушек, состоящих из пяти ячеек. В одной кормушке сыр только в одной ячейке, в другой – в четырёх. Событие А – съесть кусочек сыра. Какова вероятность события А? Каковы вероятности того, что второй раз мышка побежит к первой корзине, ко второй корзине?
Рассмотрим гипотезы: Н1 – мышка бежит к первой кормушке, Н2 – мышка бежит ко второй кормушке. Р(Н1) =1/2 = Р(Н2) (априорные вероятности) 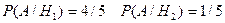 .
. 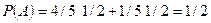
Р(Н1/A) 
Р(Н2/A) 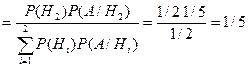 (апостериорные вероятности).
(апостериорные вероятности).
При втором подходе 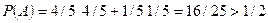 , то есть мышка обучилась, второй раз она выберет первую кормушку с большей вероятностью и добьется большего успеха.
, то есть мышка обучилась, второй раз она выберет первую кормушку с большей вероятностью и добьется большего успеха.
Это – один из основных принципов обучения кибернетических систем.
Схемы испытаний
Напомним, что опытом в теории вероятностей называют контролируемое осуществление некоторого комплекса условий S, которое можно повторить неограниченное число раз. Пусть производится n опытов (испытаний), в каждом из которых может наступить один из N исходов. Определение 1. Если результаты одного испытания не зависят от результатов других испытаний, то такие испытания называются независимыми.
Пример. В урне 3 белых и 4 чёрных шара. Вынимают 2 шара по очереди. Событие А – вытащить 1й шар белый B и второй белый. Событие В – вытащить 2й шар белый. Покажем, что события А и В зависимы. 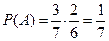 ,
, 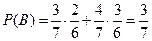 ,
, 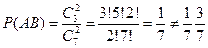 .
.
Возможны две ситуации: условия проведения испытаний не меняются (ситуация А) или меняются от испытания к испытанию (ситуация В).
Определение 2. Схема независимых испытаний с неизменными условиями и с двумя исходами в каждом из которых некоторое случайное событие А наступает с одной и той же вероятностью p = P(A), не изменяющейся от испытания к испытанию, называется схемой Бернулли.
Схема Бернулли отвечает на следующие группы вопросов:
I. Какова вероятность того, что в серии из 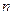 независимых испытаний событие
независимых испытаний событие 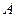 появится ровно
появится ровно 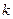 раз. В этом случае любой исход n испытаний Бернулли представляет собой последовательность длины n, состоящую из k "успехов" и (n – k) "неуспехов". Вероятность каждого такого исхода по теореме умножения независимых случайных событий равна pk(1 - p)n-k или pkqn-k, где q=1 - p. Число таких комбинаций равно числу способов выбора k мест из n для "успеха". Тогда
раз. В этом случае любой исход n испытаний Бернулли представляет собой последовательность длины n, состоящую из k "успехов" и (n – k) "неуспехов". Вероятность каждого такого исхода по теореме умножения независимых случайных событий равна pk(1 - p)n-k или pkqn-k, где q=1 - p. Число таких комбинаций равно числу способов выбора k мест из n для "успеха". Тогда 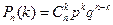
 формула Бернулли.
формула Бернулли.
Пример. Какова вероятность с пяти раз вытащить из колоды в 36 карт ровно три туза? Карты каждый раз возвращаются в колоду. 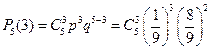
Пример. Что вероятнее: выиграть у равносильного противника в шахматы 2 партии из трех или 3 партии из четырех? Р3(2)= 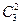 (1/2)2(1/2) = 3/8, Р4(3) =
(1/2)2(1/2) = 3/8, Р4(3) = 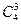 (1/2)3(1/2) = 1/4. То есть вероятнее выиграть 2 партии из трех.
(1/2)3(1/2) = 1/4. То есть вероятнее выиграть 2 партии из трех.
Приближения. При большом числе n повторных испытаний использование формулы Бернулли затруднительно в связи с необходимостью выполнения действий над очень большими числами.
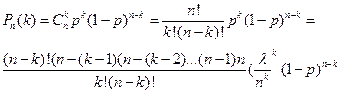
Случайные величины
Случайная величина – это величина (число), которая в результате опыта может принимать то или иное значение.
Более строго, случайная величина – это числовая функция случайного события. 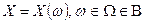
Случайная величина называется дискретной, если множество ее значений конечно или счетно. Здесь 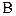 - алгебра событий. Например, число очков на грани брошенной кости, число бросков монеты до появления герба – дискретные случайные величины.
- алгебра событий. Например, число очков на грани брошенной кости, число бросков монеты до появления герба – дискретные случайные величины.
Случайная величина называется непрерывной, если ее значения заполняют некоторый интервал, возможно, бесконечный. Здесь 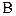 - сигма - алгебра событий. Например, расстояние от центра мишени при стрельбе, время до отказа прибора, ошибка измерения – непрерывные случайные величины.
- сигма - алгебра событий. Например, расстояние от центра мишени при стрельбе, время до отказа прибора, ошибка измерения – непрерывные случайные величины.
Рассмотрим дискретную случайную величину, принимающую значения 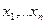 . Имеем полную группу (иначе, не все значения учтены) несовместных событий
. Имеем полную группу (иначе, не все значения учтены) несовместных событий 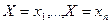 . Вероятности этих событий равны соответственно
. Вероятности этих событий равны соответственно 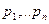
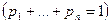 . Будем говорить, что дискретная случайная величина
. Будем говорить, что дискретная случайная величина 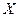 принимает значения
принимает значения 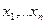 с вероятностями
с вероятностями 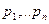 .
.
Законом распределения дискретнойслучайнойвеличины называется любое соотношение, устанавливающее зависимость между ее значениями 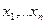 и вероятностями
и вероятностями 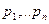 , с которыми эти значения достигаются.
, с которыми эти значения достигаются.
Основные формы закона распределения дискретной случайной величины: ряд распределения – таблица
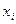
| 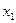
| ….. 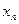
|
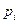
| 
| ….. 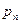
|
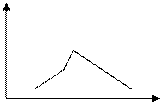
 многоугольник распределения
многоугольник распределения
p3
p2
p1, pn
x1 x2 x3 …xn
Можно задать закон распределения в виде аналитической зависимости, связывающей значения 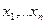 и вероятности
и вероятности 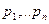 .
.
Рассмотрим непрерывную случайную величину. Для непрерывной случайной величины 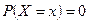 , поэтому рассматривают события
, поэтому рассматривают события 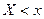 и вероятности этих событий.
и вероятности этих событий.
Функцией распределения непрерывной случайной величины 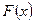 называется вероятность события
называется вероятность события 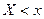 .
. 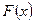 =
= 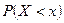 .
.
Дата добавления: 2016-07-27; просмотров: 2881;











