Простые расширения полей

Пусть поле P содержится в поле T и a – элемент T не принадлежащий P. Рассмотрим наименьшее поле P(a) содержащее все элементы из P и a. Все элементы вида 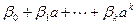принадлежат P(a). Рассмотрим два случая.

1. Ни один элемент вида 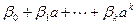не равен 0. Тогда поле P(a) изоморфно полю частных P(x). В этом случае говорят о трансцендентном расширении полей.
2. Найдется 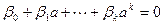. Выберем элемент с наименьшей степенью. Многочлен 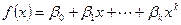неприводим и поле P(a) изоморфно факторкольцу 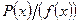. В этом случае говорят об алгебраическом расширение полей.

Конечные поля.

Теорема 4.2. Число элементов конечного поля pⁿ, где p – простое число.

Доказательство. Поскольку поле P конечно, то его характеристика отлична от нуля. Пусть p его характеристика. Поле P, можно рассматривать как векторное пространство над Z_p. Обозначим через v₁,…,v_n базис P. Любой элемент поля P однозначно характеризуется координатами (x₁,…,x_n ) в этом базисе. Каждая координата принимает p значений, следовательно, число различных наборов координат, а значит и элементов поля P, равно pⁿ.

Лемма 4.1 В поле характеристики p .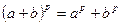

Доказательство. 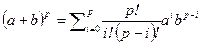, где 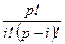- кратность вхождения элемента. Величина 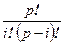не делится на p только в случае i=0;p. Так как pe=0, то .

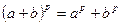Теорема 4.3. Для любого натурального n и простого p существует поле порядка pⁿ.

Расширим Z_p так, чтобы результирующее поле содержало все корни многочлена 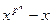. Многочлен не имеет кратных корней, так как его производная равна –1. Обозначим через M множество корней многочлена 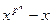. Легко проверить, что M является полем и число его элементов равно pⁿ

Теорема 4.4. Поле порядка 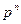единственно с точностью до изоморфизма.

Доказательство.

Поскольку число элементов поля 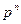, то его характеристика равна 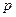. Следовательно, любое поле P порядка 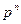можно рассматривать как расширение кольца вычетов 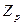. Мултьипликативная группа поля ( 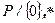) имеет порядок 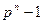, и, следовательно, для любого 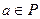справедливо 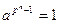. Таким образом, все элементы поля являются корнями уравнения 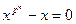над .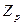

Теорема 4.5. Мультипликативная группа корней n-ой степени из 1 в поле P является цикличной.

Доказательство. Пусть p характеристика поля P. Если 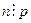, то 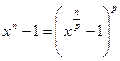, и, значит, множество корней уравнения 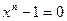совпадает с множеством корней степени 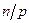. Не нарушая общности можно считать 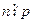. Доказательство достаточно провести для случая, когда все корни n-ой степени из 1 содержатся в поле P. В противном случае расширим поле и воспользуемся фактом, что любая подгруппа циклической группы – циклическая. Поскольку 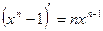имеет только единственный корень, равный нулю, то количество корней n-ой степени из 1 равно n. Рассмотрим три случая:

1. n – простое число. Тогда группа корней имеет порядок n, и, значит циклическая

2. 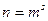- степень простого числа. Найдем корень 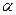уравнения 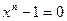, не являющийся корнем уравнения 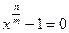. Порядок элемента 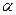является делителем порядка группы n и не является делителем 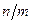. Следовательно, порядок 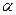равен n и группа циклическая.

3. Пусть 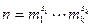. Обозначим через 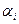порождающий элемент циклической группы корней из 1 степени 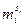. Положим 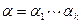. Индукцией по k покажем, что порядок 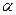равен 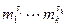. При k=1 утверждение очевидно. Пусть оно доказано для k-1. Порядок элемента 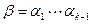равен 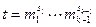. Наибольший общий делитель t и 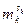равен 1, и, значит, найдутся числа u и v, что 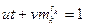. Поскольку 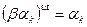и 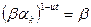, то порядок элемента 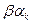делится на t и на 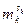. Далее, из равенства 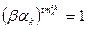, следует, что порядок элемента 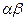является делителем 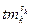. Теорема доказана.

Теория Галуа

Поле T называется конечным расширением поля P, если T является конечно мерным линейным пространством над P. Размерность пространства называется степенью расширения.

Любое алгебраическое расширение поля P является конечным. Его степень равна степени неприводимого многочлена.

Теорема 5.1. Конечное расширение U поля T, являющегося конечным расширением поля P, является конечным расширением P. Причем степень расширения U над P равна произведению степеней расширения.

Доказательство. Почти очевидно.

Элемент поля T называется алгебраичным над P, если он является корнем некоторого многочлена над P.

Все элементы конечного расширения P алгебраичны над P.

Любое конечное расширение может быть получено с помощью присоединения конечного числа алгебраических расширений.

Теорема 5.2. Любое конечное расширение поля P характеристики 0 является простым расширением.

Доказательство не очевидно.

Конечное расширение T называется нормальным расширением P, если из факта, что неприводимый многочлен над P имеет в T корень, следует его разложимость на линейные множители. Ясно, что нормальное расширение поля характеристики 0, является полем разложения многочлена. Верно и обратное утверждение. Поле разложения многочлена является нормальным расширением.

Автоморфизмом поля называется изоморфное отображение само на себя.

Группой Галуа нормального расширения T поля P называется группа автоморфизмов поля T, сохраняющая элементы поля P.

Теорема 5.3. Каждому промежуточному полю U, 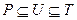соответствует некоторая подгруппа 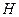группы Галуа, а именно, совокупность тех автоморфизмов, которые не меняют элементы 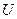. Поле 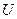определяется подгруппой 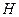однозначно.

6 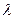-матрицы.