Закон нормального распределения случайных погрешностей изготовления.

Под погрешностью изготовления понимается разность между действительным размером детали и наилучшим, т.е. обеспечивающим оптимальное функционирование изделия. Обычно наилучший размер расположен в середине поля допуска:

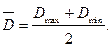(3.1)

Точность - степень приближения действительного размера детали к оптимальному.

Пусть изготовлена партия из n деталей по одному и тому же чертежу. В силу случайных погрешностей размеры деталей в партии отличаются друг от друга. Если причины появления погрешностей носят случайный характер, например отклонение температуры окружающей среды, неоднородность физико-механических свойств материала заготовки, разброс в режимах обработки в связи с неточностью их воспроизведения станком, то такие погрешности называются случайными. Пусть каждая из этих деталей имеет некоторый диаметр D_i ( 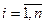), отягощенный случайной погрешностью. В большинстве случаев распределение изготовленных деталей, например по D, отвечает закону нормального распределения погрешностей или закону Гаусса:

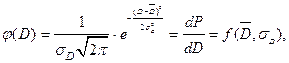(3.2)

где

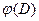- плотность вероятности;

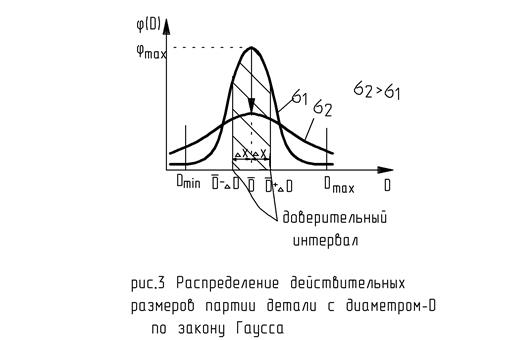
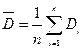- математическое ожидание, ;

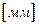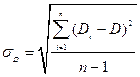- среднее квадратичное отклонение, ;

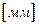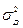- дисперсия, параметр, характеризующий величину случайных погрешностей.

Анализируя формулу (3.2), можно убедиться, что плотность вероятности достигает максимума при :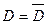

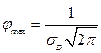; (3.3)

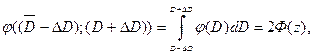(3.4)

где

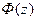- функция Лапласа;

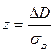- квантиль Гаусса;

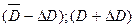( ) - доверительный интервал.

Приведем некоторые распространенные значения функции Лапласа:

;

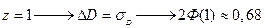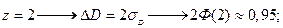
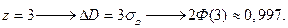
Площадь под кривой (вероятность появления значения измеренной величины) в интервале от -∞ до +∞ всегда равна единице (рис. 3).

В технологии обычно выбирают такое оборудование, чтобы вероятность появления действительного размера детали внутри интервала 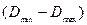составляла 0,997. В этом случае:

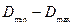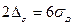= , (3.5)

где

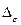- доверительный интервал.

Для большинства производств выполняется это правило- правило 6σ.