Фермионы и бозоны. Распределение Ферми-Дирака и Бозе-Эйнштейна

Согласно современной квантовой теории все элементарные и сложные частицы, а также квазичастицы разделяются на два класса - фермионы и бозоны.

К фермионам относятся электроны, протоны, нейтроны и все другие частицы, имеющие полуцелые проекции спина, т.е. L_SZ=±(2n+1) 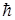/2 , где n=0, 1, 2 ... - целые числа. Напомним, что спин (spin) L_S - это собственный момент импульса частиц, имеющий квантовую природу.

К бозонам относятся фотоны, некоторые ядра атомов, квазичастицы: фононы, магноны, плазмоны, экситоны. Все они имеют проекцию спина либо равную нулю, либо равную целому числу 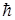, т.е. L_SZ=±n 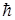. Фермионы и бозоны имеют различные свойства.

7.3.1. Фермионы

Они подчиняются принципу Паули - в одном квантовом состоянии может находится не более одного фермиона (или в одном квантовом состоянии может находиться только один фермион). Т.е. фермионы - индивидуалисты. Система фермионов описывается распределением Ферми-Дирака: среднее число фермионов <n_i>, приходящееся на одно квантовое состояние с данной энергией Е_i

<n_i>= 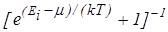, (1)

где k - постоянная Больцмана, Т - термодинамическая температура, m - химический потенциал.

Поясним физический смысл химического потенциала. Известно, что первое начало термодинамики для системы с переменным числом частиц N имеет вид

dQ=dU+dA-mdN, (2)

отсюда изменение внутренней энергии dU=ТdS-PdV+mdN. Таким образом, слагаемое mdN учитывает изменение внутренней энергии системы за счет изменения числа частиц на dN. Пусть протекает адиабатический (dQ=ТdS=0) изохорический (dV=0) процесс, тогда dU=mdN и химический потенциал m= (dU /dN)_{S, V},

т. е. он характеризует изменение внутренней энергии системы dU при добавлении в систему одной частицы, когда система при этом не получала тепла и не совершала работу; m зависит от внешних параметров V, T и числа частиц N. Для фермионов m>0.

На рис. 1(а) сплошной кривой представлено распределение Ферми-Дирака.

Если Т®0, то из (1) следует:

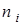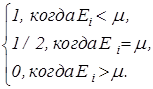á ñ = (3)

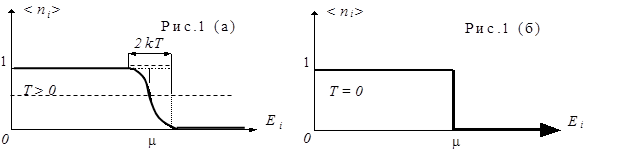Это значит, что при Т = 0 частицы Ферми - газа заполняют все квантовые состояния с энергиями 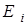< m . Квантовые состояния с более высокими энергиями не заполнены. Кривая распределения вырождается в прямоугольник (рис. 1б). Значение энергии, ниже которой все состояния системы частиц фермионов при Т = 0 К заняты, называется энергией Ферми . Для идеального ферми газа 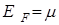при Т = 0 К. Можно показать это

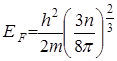, (4)

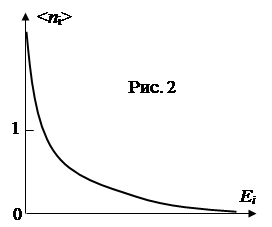где m и n - масса и концентрация фермионов. Следовательно, максимальная энергия, которую могут иметь электроны в металле при Т = 0 К, равна энергии Ферми 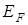. Для хорошо проводящих металлов 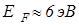, для полупроводников - значительно меньше

7.3.2. Бозоны

Они не подчиняются принципу Паули, т. е. в одном квантовом состоянии может быть много бозонов, т. е. бозоны - коллективисты. Система бозонов описывается распределением Бозе-Эйнштейна: среднее число бозонов á 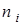ñ, приходящееся на одно квантовое состояние с энергией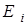

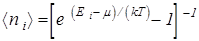(5)

Поскольку числа заполнения á 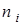ñ не могут быть отрицательными, то из (5) следует, что для бозонов m £0. Распределение Бозе-газа представлено на рис.2.