Классическая теория теплоемкости кристаллов. Закон Дюлонга и Пти

Простейшей моделью кристалла является правильно построенная кристаллическая решетка, в узлах которой помещаются атомы (или ионы, молекулы), принимаемые за материальные точки. Атом совершает тепловые колебания около положения равновесия. Если колебания малы, то они будут гармоническими. Энергия каждого атома слагается из потенциальной W_п и кинетической W_к. Известно [ cм. конспект лекций Физика, ч. I, лекции 11, 12 формулы (7), (8)], что в случае гармонических колебаний

W_п=(1/2) kA²cos²(wt+q)=(1/4) kA²[1+cos2(wt+q)], (1)

W_к=(1/2) kA²sin²(wt+q)=(1/4) kA²[1-сos2(wt+q)].

Рис. 1

Так как cos2(wt+q) c равной вероятностью принимают как положительные так и отрицательные значения и поэтому при усреднении обращается в нуль, то <W_K>=<W_n>=(1/4)kA².

В лекции 4 показано, что на каждую степень свободы приходиться в среднем кинетическая энергия (1/2)kT. Атом имеет 3 степени свободы, поэтому <W_K>=<W_n>=(3/2)kT. Таким образом средняя энергия атома <Е>=<W_K>+<W_n>=3kT. Умножив эту величину на постоянную Авогадро N_A (число атомов в моле вещества), найдем внутреннюю энергию моля твердого тела

U=3kTN_A=3RT, (2)

где R=kN_A=8.31 Дж/мольК - универсальная газовая постоянная. Отсюда молярная теплоемкость твердого тела

C=dU/dT=3R»25 Дж/(моль×К). (3)

Этотзакон был эмпирически (опытным путем) установлен в 1919 г. Дюлонгом и Пти. Он утверждает:

Молярная теплоемкость для всех простых твердых тел равна 3R, т.е.

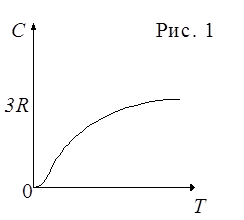C=3R. (4)

Для многих веществ этот закон хорошо выполняется, хотя некоторые вещества (алмаз С, Ве, В) имеют значительные отклонения от вычисленных теплоёмкостей. Опыт также показал, что С зависит от температуры и вблизи нуля кельвин для всех веществ С~­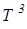 . На рис. 1 представлена характерная экспериментально полученная зависимость С от Т. Расхождение опытных и теоретических значений теплоёмкостей объяснили, исходя из квантовой теории теплоёмкости, Эйнштейн и Дебай.