Основные сведения о нелинейных РАС
При исследовании РАС необходимо уметь анализировать их поведение не только в линейном, но и в нелинейном режиме. Работа в нелинейном режиме наблюдается, например, при выходе ошибки дискриминатора за пределы линейного участка дискриминационной характеристики (например, из-за интенсивных помех – в этом случае потребуется оценивать условия, при которых может наступить срыв слежения), при переходе усилительного каскада в режим ограничения и т. п. Кроме того, некоторые элементы РАС не могут быть линеаризованы (например, релейный элемент; дискриминационные характеристики принципиально являются нелинейными) [1].
В таких случаях процессы в РАС описываются нелинейными дифференциальными уравнениями, что существенно усложняет их анализ.
При составлении дифференциального уравнения нелинейных РАС сначала составляют уравнения для каждого устройства системы. Хотя бы один элемент в такой системе будет иметь нелинейную характеристику.
Устройства, допускающие линеаризацию, образуют линейную частьРАС, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть.
Во многих случаях нелинейные элементы можно представить как статические, зависимость выходного сигнала от входного в которых описывается нелинейной зависимостью вида у = F(x).
Характерной особенностью нелинейных систем является возможность возникновения в них автоколебаний. Исследование условий возникновения автоколебаний, их устойчивости и параметров (амплитуды и частоты) является одной из задач анализа нелинейных систем.
В нелинейных РАС проявляются новые эффекты и свойства: синхронизация, неприменимость принципа суперпозиции, захват (полоса захвата), слежение (полоса удержания), срыв слежения и сопровождения
и т. п.
В настоящее время не создано общей теории анализа нелинейных РАС, а разработанные методы позволяют решать лишь отдельные нелинейные задачи. Точные решения нелинейных дифференциальных уравнений известны лишь для систем первого порядка и некоторых систем второго. Поэтому в анализе РАС широко используются приближенные и вычислительные методы.
Для нелинейных РАС понятие устойчивости усложняется. Вводятся понятия локальной и глобальной устойчивости, а также понятие устойчивости системы в целом.
Различают статические и динамические нелинейные звенья.
Статические описываются алгебраическими уравнениями, а динамические – дифференциальными.
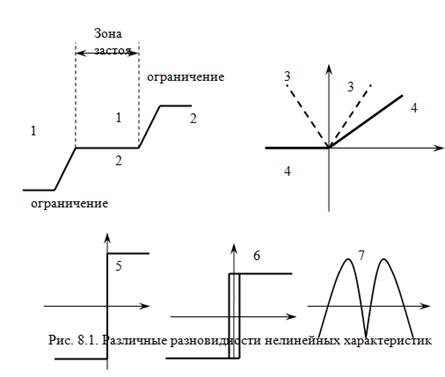
На рис. 8.1 приведены примеры некоторых нелинейных характеристик элементов РАС.
Характеристики нелинейных звеньев могут быть
– симметричными (например, графики 1 и 2) и несимметричными (график 4);
– непрерывными (график 7) и кусочно-ломаными (например, графики 1, 2 и 4);
– однозначными и неоднозначными (график 7).
Некоторые нелинейности являются существенными (5, 6, 7), другие допускают при определенных условиях линеаризацию. Характеристика, представленная графиком 7, характерна для фазового дискриминатора.
Ограниченность апертуры характеристики дискриминатора кроме возможного проявления срыва слежения определяет и другую проблему – обеспечение надежного захвата сигнала следящей РАС и надежного сопровождения цели.
При анализе нелинейных РАС важное значение имеет место включения нелинейного элемента и его сочетания с линейными инерционными звеньями. Обычно выделяют существенные нелинейности.
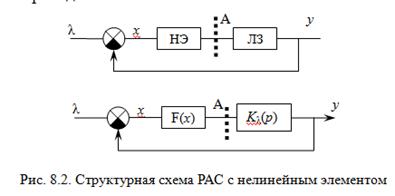
В результате нелинейные РАС сводят к виду, приведенному на
рис. 8.2.
Анализ РАС проводят относительно точки «А».
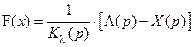 .
.
Дата добавления: 2020-10-25; просмотров: 587;











