Метод статистической линеаризации.

Идея метода основана на приближенной замене нелинейных преобразований процессов, происходящих в системе, статистически эквивалентными им линейными преобразованиями. В результате такой замены система линеаризуется и для ее исследования можно применять аппарат линейной теории. Данный метод может быть применен только для нелинейных элементов с однозначной характеристикой. При использовании метода статистической линеаризации предполагают, что закон распределения случайной величины нормальный. Такое предположение может быть сделано исходя из того факта, что любое реальное инерционное звено (т. е. обладающее свойствами фильтра) имеет тенденцию к «нормализации» закона распределения случайного процесса.

Основным критерием при статистической линеаризации является критерий равенства мат. ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента.

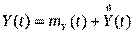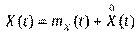Обозначим случайный процесс на входе и на выходе нелинейного элемента как и соответственно, где 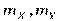- мат. ожидание, - центрированный случайный процесс.

При статистической линеаризации сигнал на выходе эквивалентного линейного элемента представляют как

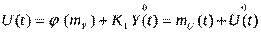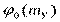, где - мат. ожидание нелинейной функции 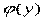, 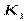- эквивалентный статистический коэффициент усиления по случайной центрированной составляющей.

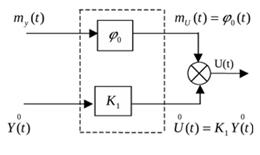
Если нелинейный элемент имеет нечетную характеристику ,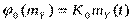

где - эквивалентный статистический коэффициент усиления нелинейного элемента по мат. ожиданию (по случайной составляющей). Как видно, в этом случае нелинейный элемент был заменен двумя линейными элементами с коэффициентами усиления .

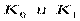Как было отмечено, критерием статистической эквивалентности является равенство мат. ожидания и дисперсий на выходе нелинейного элемента и эквивалентного ему линейного элемента:

.

Для нечетных нелинейностей .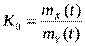

Для определения коэффициента рассмотрим уравнение:

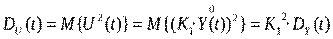
откуда , где 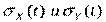- среднеквадратические отклонения.

и плотность вероятности Ф(Y) случайного сигнала Y(t) на входе нелинейного элемента.j Статистические коэффициенты можно также выразить через нелинейную зависимость

Метод статистической линеаризации наиболее часто используется при предположении о стационарности случайного процесса. В этом случае и коэффициенты статистической линеаризации не зависят от времени. При этом линеаризованная система является системой с постоянными параметрами и её исследование может быть проведено сравнительно просто.

При рассмотрении нестационарных процессов статистическая линеаризация не дает преимуществ в анализе нелинейной системы, так как при этом коэффициенты линеаризации меняются во времени, то есть линеаризованная система представляет собой систему с переменными параметрами.